Find the square root of each of the following numbers by Division method.
(i) 2304 (ii) 4489 (iii) 3481 (iv) 529 (v) 3249 (vi) 1369 (vii) 5776 (viii) 7921 (ix) 576 (x) 1024 (xi) 3136 (xii) 900
Solution:
What is known: Perfect Squares
What is unknown: Square root by using the division method.
Reasoning: When a number is large, even the method of trading the square root by prime factorization becomes lengthy and difficult, so the division method is used.
Steps:
(i)
The square root of 2304 is calculated as follows.

Since the remainder is zero, we can conclude that
√2304 = 48
(ii)

√4489 = 67
(iii)

√3481 = 59
(iv)

√529 = 23
(v)

√3249 = 57
(vi)
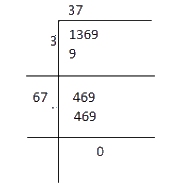
Therefore,
√1369 = 37
(vii)

Therefore,
√5776 = 76
(viii)

√7921 = 89
(ix)

√576 = 24
(x)

√1024 = 32
(xi)

√3136 = 56
(xii)
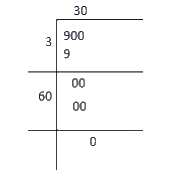
√900 = 30
☛ Check: NCERT Solutions for Class 8 Maths Chapter 6
Video Solution:
Find the square root of each of the following numbers by Division method. (i) 2304 (ii) 4489 (iii) 3481 (iv) 529 (v) 3249 (vi) 1369 (vii) 5776 (viii) 7921 (ix) 576 (x) 1024 (xi) 3136 (xii) 900
NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.4 Question 1
Square roots of the following numbers using prime factorisation method (i) 48 (ii) 67 (iii) 59 (iv) 23 (v) 57 (vi) 37 (vii) 76 (viii) 89 (ix) 24 (x) 32 (xi) 56 (xii) 30
☛ Related Questions:
- Find the number of digits in the square root of each of the following numbers (without any calculation). (i) 64 (ii) 144 (iii) 4489 (iv) 27225 (v) 390625
- Find the square root of the following decimal numbers. (i) 2.56 (ii) 7.29 (iii) 51.84 (iv) 42.25 (v) 31.36
- Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained. (i) 402 (ii) 1989 (iii) 3250 (iv) 825 (v) 4000
- Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained. (i) 525 (ii) 1750 (iii) 252 (iv) 1825 (v) 6412
visual curriculum
