Find the roots of the following equations:
(i) x - 1/x = 3, x ≠ 0
(ii) 1/(x + 4) - 1/(x - 7) = 11/30, x ≠ - 4, 7

Solution:

Convert the given equation in the standard form i.e, ax² + bx + c = 0 and by using the quadratic formula, find the roots.

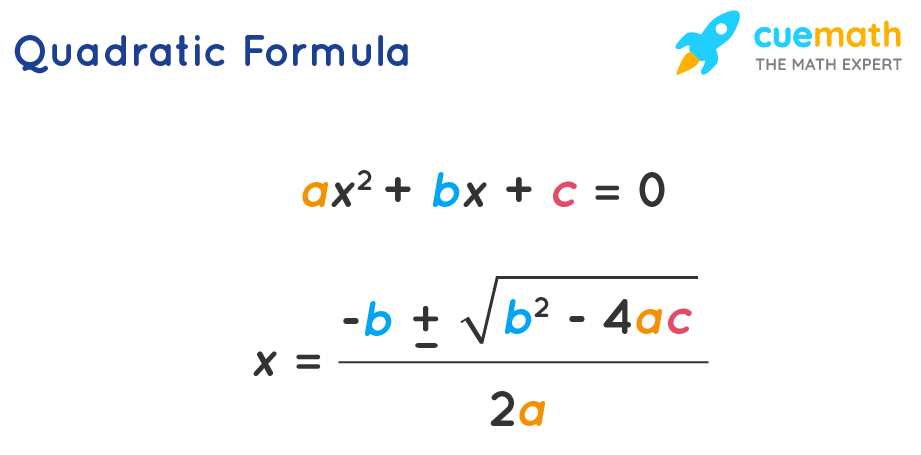
(i) x - 1/x = 3, x ≠ 0

x - 1/x = 3

Multiplying x on both the sides

x² - 1 = 3x 

x² - 3x - 1 = 0

Comparing x² - 3x - 1 = 0 against the standard form of quadratic equation that is ax² + bx + c = 0,

We find that a = 1, b = - 3, c = - 1

b² - 4ac = (-3)² - 4(1)(-1)

= 9 + 4

= 13 > 0

Therefore, x = (- b ± √b² - 4ac) / 2a

x = (3 ± √13) / 2

The roots are (3 + √13) / 2, (3 - √13) / 2

(ii) 1/(x + 4) - 1/(x - 7) = 11/ 30, x ≠ - 4, 7

[(x - 7) - (x + 4)] / (x + 4)(x - 7) = 11/ 30

[x - 7 - x - 4] / x² + 4x - 7x - 28 = 11/ 30

(- 11) / (x² - 3x - 28) = 11/30

- 11 × 30 = 11(x² - 3x - 28)

- 30 = (x² - 3x - 28) [Cancelling 11 from both sides of the equation ]

x² - 3x - 28 + 30 = 0

x² - 3x + 2 = 0

Comparing x² - 3x + 2 = 0 against the standard form ax² - bx + c = 0 ,

We find that a = 1, b = - 3 and c = 2

b² - 4ac = (-3)² - 4(1)(2)

= 9 - 8

= 1 > 0

Therefore, real roots exist for this quadratic equation.

Therefore, x = (- b ± √b² - 4ac) / 2a

x = (3 ± √1) / 2

x = (3 + 1)/2 and x = (3 - 1)/2

x = 4 / 2 and x = 2 / 2

x = 2 and x = 1

Therefore, roots are 2, 1.

☛ Check: NCERT Solutions for Class 10 Maths Chapter 4

---

Video Solution:

Find the roots of the following equations: (i) x - 1/x = 3, x ≠ 0 (ii) 1/(x + 4) - 1/(x - 7) = 11/30, x ≠ - 4, 7

Class 10 Maths NCERT Solutions Chapter 4 Exercise 4.3 Question 3

Summary:

The roots of the following equations are (i) x - 1/x = 3, x ≠ 0 are x = 3 + √13 / 2 or x = 3 - √13 / 2 and (ii) 1/(x + 4) - 1/(x - 7) = 11/30, x ≠ - 4, 7 are 2 and 1.

---

☛ Related Questions:

• The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is 1/3. Find his present age.
• In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had She got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
• The diagonal of a rectangular field is 60 meters more than the shorter side. If the longer side is 30 meters more than the shorter side, find the sides of the fields.
• The difference of squares of two numbers is 180. The square of a smaller number is 8 times the larger number. Find the two numbers.