A day full of math games & activities. Find one near you.

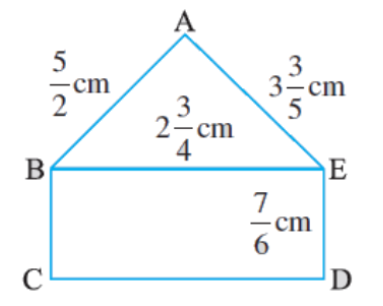
Find the perimeters of (i) ∆ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?

Solution:

Perimeters of the rectangle and triangle can be calculated by adding lengths of four sides of the rectangle and the three sides of the triangle. Perimeters can be compared to decide whose perimeter is greater.

Steps:

i) Perimeter of ΔABE = sum of all its sides = AB + BE + AE

= (5/2) + \(2{\Large\frac{3}{4}}\) + \(3{\Large\frac{3}{5}}\)

= (5/2) + (11/4) + (18/5)

The LCM of 2, 4, 5 = 20

= [(5/2) × (10/10)] + [(11/4) × (5/5)] + [(18/5) × (4/4)]

= (50/20) + (55/20) + (72/20)

= (50 + 55 + 72)/20

= 177/20

= \(8{\Large\frac{17}{20}}\)cm

(ii) In rectangle, BCDE

Perimeter of the rectangle = 2 × (length + breadth)

= 2 × (BE + ED)

= 2 × [(11/4) + (7/6)]

The LCM of 4, 6 = 12

= 2 × {[(11/4) × (3/3)] + [(7/6) × (2/2)]}

= 2 × [(33/12) + (14/12)]

= 2 × [(33 + 14)/12]

= 2 × (47/12)

= 47/6

= \(7{\Large\frac{5}{6}}\) cm

On comparing,

\(8{\Large\frac{17}{20}}\) > \(7{\Large\frac{5}{6}}\)

Therefore, the perimeter of ΔABE is greater than the perimeter of rectangle BCDE.

☛ Check: NCERT Solutions for Class 7 Maths Chapter 2

Video Solution:

Find the perimeters of (i) ∆ABE (ii) the rectangle BCDE in this figure. Whose perimeter is greater?

NCERT Solutions Class 7 Maths Chapter 2 Exercise 2.1 Question 5

Summary:

The perimeters of (i) ∆ABE is \(8{\Large\frac{17}{20}}\) cm and (ii) the rectangle BCDE \(7{\Large\frac{5}{6}}\). Therefore, perimeter of ΔABE is greater than the perimeter of rectangle BCDE.

☛ Related Questions: