Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case

Solution:

We will be using the concept of LCM(Least Common Multiple) to solve this.

To determine the least number which when divided by 6, 15, and 18 leave the remainder 5 in each case,we need to find the LCM of the three given numbers.

Since, the LCM obtained will be the smallest common multiple of all the three numbers 6, 15, and 18, after getting LCM we need to add 5  to it so as to get 5 as a remainder.

Let's find the LCM of 6, 5 and 18 as shown below.

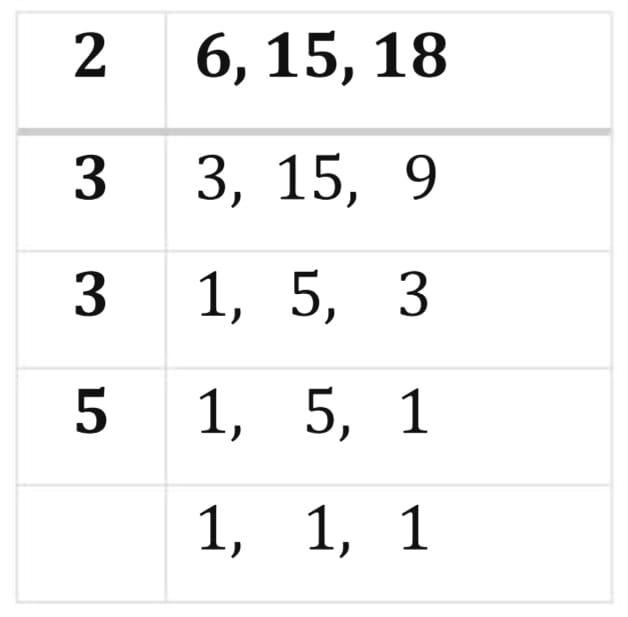
Therefore, LCM of 6, 15 and 18 = 2 × 3 × 3 × 5 = 90.

Thus we can see that, 90 is the least number exactly divisible by 6, 15, and 18.

To get a remainder 5, we need to add 5 to the LCM.

⇒ 90 + 5 = 95.

Thus, when 95 is divided by 6, 15, and 18 we get a remainder of 5 in each case.

Hence, the required number for the given problem is 95.

You can also use the LCM Calculator to solve this.

NCERT Solutions for Class 6 Maths Chapter 3 Exercise 3.7 Question 8

Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case

Summary:

The least number which when divided by 6, 15, and 18 leaving a remainder of 5 in each case will be 95.

☛ Related Questions:

• Determine The Smallest 3 Digit Number Which Is Exactly Divisible By 6 8 And 12
• Determine The Greatest 3 Digit Number Exactly Divisible By 8 10 And 12
• The Traffic Lights At Three Different Road Crossings Change After Every 48 Seconds 72 Seconds And 108 Seconds Respectively If They Change Simultaneously At 7 Am At What Time
• Three Tankers Contain 403 Litres 434 Litres And 465 Litres Of Diesel Respectively Find The Maximum Capacity Of A Container That Can Measure The Diesel Of The Three Containers