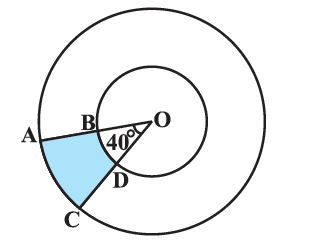
Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠ AOC = 40°.
Solution:
We use the concepts related to areas of sectors of circles and concentric circles.
In a circle with radius r and the angle at the centre with degree measure θ,
Area of the sector = θ/360° × πr2
The area of the shaded region can be calculated by subtracting the area of the sector of the smaller circle from the area of the sector of the larger circle.
Area of shaded region ABDC = Area of sector ACO - Area of sector BDO
Radius of the larger circle, R = OA = 14cm
Radius of the smaller circle, r = OB = 7cm
The angle at the centre, θ = 40°
Area of shaded region ABDC = Area of sector ACO - Area of sector BDO
= θ/360° × πR2 - θ/360° × πr2
= θ/360° π (R2 - r2)
= θ/360° π (R + r )(R - r)
= 40°/360° × 22/7 × (14 + 7) (14 - 7)
= 1/9 × 22/7 × 21 × 7
= (22 × 21 × 7)/(9 × 7)
= (22 × 7)/3
= 154/3 cm2
☛ Check: NCERT Solutions for Class 10 Maths Chapter 12
Video Solution:
Find the area of the shaded region in Fig. 12.20, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠ AOC = 40°.
NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.3 Question 2
Summary:
The area of the shaded region in the figure if the radii of the two concentric circles with center O are 7 cm and 14 cm respectively and ∠AOC = 40° is 154/3 cm2.
☛ Related Questions:
- Find the area of the shaded region in Fig. 12.21, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
- Find the area of the shaded region in Fig. 12.22, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as centre.
- From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.23. Find the area of the remaining portion of the square.
- In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design.
visual curriculum
