Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° - sin² 60°
(iii) cos 45°/(sec 30° + cosec 30°)
(iv) (sin 30° + tan 45° - cosec 60°) /(sec 30° + cos 60° + cot 45°)
(v) (5cos² 60° + 4sec² 30° - tan² 45°)/(sin² 30° + cos² 30°)

Solution:

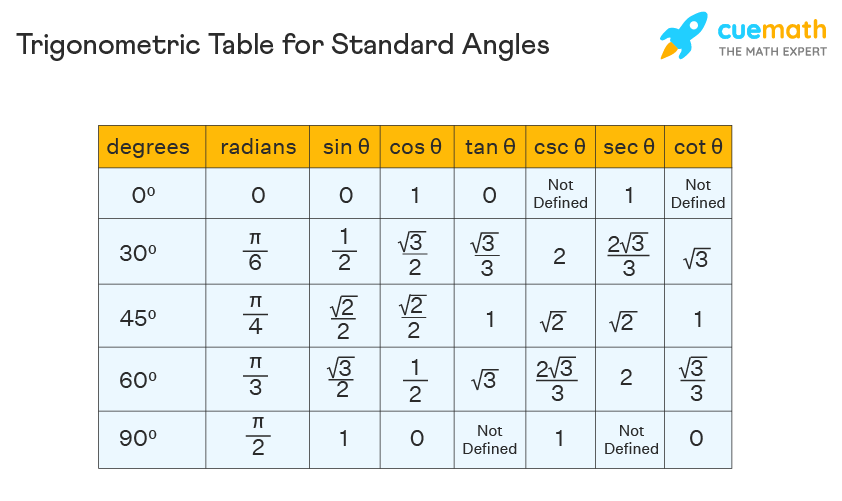
We will use the six basic trigonometric ratios and trigonometric table to solve the problem.

(i) sin 60° cos30° + sin 30° cos 60°

= (√3/2)(√3/2) + (1/2)(1/2)

= 3/4 + 1/4

= (3 + 1)/4

= 4/4

= 1

(ii) 2 tan² 45° + cos² 30° - sin² 60° 

= 2(1)² + (√3/2)² - (√3/2)²

= 2 + 3/4 - 3/4

= 2

(iii) cos 45°/(sec 30° + cosec 30°)

= (1/√2) / [(2/√3) + 2]

= (1/√2) / [(2 + 2√3)/√3]

= (1 × √3) / [√2 × (2 + 2√3)]

= √3 / [2√2(√3 + 1)]

Multiplying numerator and denominator by √2 (√3 - 1), we get

= √3 / [2√2(√3 + 1)] × √2 (√3 - 1) / √2 (√3 - 1)

= (3√2 - √6) / 4(3 - 1)

= (3√2 - √6) / 8

(iv) (sin 30° + tan 45° - cosec 60°) / (sec 30° + cos 60° + cot 45°)

= [(1/2 + 1 - 2/√3) / (2/√3 + 1/2 + 1)]

= (3/2 - 2/√3) / (2/√3 + 3/2)

= [{(3√3 - 4)/2√3} / {(4 + 3√3)/2√3}]

= (3√3 - 4) / (3√3 + 4)

Multiplying numerator and denominator by 3√3 - 4, we get

= (3√3 - 4)(3√3 - 4) / (3√3 + 4)(3√3 - 4)

= (27 + 16 - 24√3) / (27 - 16)

= (43 - 24√3) / 11

(v) (5cos² 60° + 4sec² 30° - tan² 45°) / (sin² 30° + cos² 30°)

= [5 × (1/2)² + 4 × (2/√3)² - (1)²] / [(1/2)² + (√3/2)^{​​​​​​​2}]

= (5/4 + 16/3 - 1) / (1/4 + 3/4)

= [(15 + 64 - 12)/12] / [(3 + 1)/4]

= (67/12) / (4/4)

= 67/12

☛ Check: Class 10 Maths NCERT Solutions Chapter 8

---

Video Solution:

Evaluate the following: (i) sin 60° cos 30° + sin 30° cos 60° (ii) 2 tan² 45° + cos² 30° - sin² 60° (iii) cos 45°/(sec 30° + cosec 30°) (iv) sin 30° + tan 45° - cosec 60°/(sec 30° + cos 60° + cot 45°) (v) 5cos² 60° + 4sec² 30° - tan² 45°/(sin² 30° + cos² 30°)

Maths NCERT Solutions Class 10 Chapter 8 Exercise 8.2 Question 1

Summary:

For the following problems: (i) sin 60° cos 30° + sin 30° cos 60° = 1, (ii) 2 tan² 45° + cos² 30° - sin² 60° = 2, (iii) cos 45°/(sec 30° + cosec 30°) = (3√2 - √6)/8, (iv) (sin 30° + tan 45° - cosec 60°)/(sec 30° + cos 60° + cot 45°) = (43 - 24√3)/11, (v) (5cos² 60° + 4sec² 30° - tan² 45°)/(sin² 30° + cos² 30°) = 67/12. 

---

☛ Related Questions:

• Choose the correct option and justify your choice:(i) 2 tan 30°/1 + tan2 30°(A) sin 60° (B) cos 60° (C) tan 60° (D) sin 60°(ii) 1 - tan2 45°/1 + tan2 45°(A) tan 90° (B) 1 (C) sin 45° (D) 0°(iii) sin 2A = 2 sin A is true when A =(A) 0° (B) 30°(C) 45° (D) 60°(iv) 2 tan 30°/1 - tan2 30°(A) cos 60° (B) sin 60° (C) tan 60° (D) sin 30°
• If tan (A + B) = √3 and tan (A - B) = 1/√3; 0° < (A + B) ≤ 900 , A > B, find A and B.
• State whether the following are true or false. Justify your answer.(i) sin (A + B) = sin A + sin B.(ii) The value of sin θ increases as θ.(iii) The value of cos θ increases as θ.(iv) sin θ = cos θ for all values of θ.(v) cot A is not defined for A = 0°.