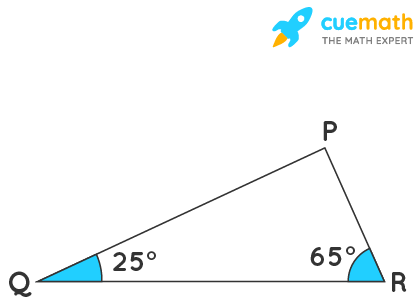
Angles Q and R of a ∆PQR are 25º and 65º. Write which of the following is true:
(i)PQ² + QR² = RP²
(ii)PQ² + RP² = QR²
(iii)RP² + QR² = PQ²

Solution:

From the figure we see that the two angles of a triangle are given and we must find out the third angle by using the angle sum property that is the sum of three interior angles of a triangle is 180°.

We know that, sum of interior angles of a triangle is 180°.

∠P + ∠Q + ∠R = 180°

∠P + 25° + 65° = 180°

∠P + 90° = 180°

∠P = 180° - 90°

∠P = 90°

Thus, triangle PQR is a right angled at P

As one of the angles is 90° that means it is a right-angled triangle and the square of the hypotenuse is equal to the sum of the square of the other two sides.

Therefore, by Pythagoras theorem,

(Perpendicular)² + (Base)² = (Hypotenuse )²

Here, Perpendicular = QP, Base = PR and Hypotenuse = QR

(QP)² + (PR)² = (QR)²

Hence, option (ii) is correct.

☛ Check: NCERT Solutions for Class 7 Maths Chapter 6

Video Solution:

Angles Q and R of a ∆PQR are 25º and 65º. Write which of the following is true: (i)PQ² + QR² = RP² (ii)PQ² + RP² = QR² (iii)RP² + QR² = PQ²

NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5 Question 6

Summary:

Angles Q and R of a ∆PQR are 25º and 65º. Option (ii) PQ² + RP² = QR² is the correct result.

☛ Related Questions:

• Pqr Is A Triangle Right Angled At P If Pq 10 Cm And Pr 24 Cm Find Qr
• Abc Is A Triangle Right Angled At C If Ab 25 Cm And Ac 7 Cm Find Bc
• A 15 M Long Ladder Reached A Window 12 M High From The Ground On Placing It Against A Wall At A Distance A Find The Distance Of The Foot Of The Ladder From The Wall
• Which Of The Following Can Be The Sides Of A Right Triangle I 25 Cm 65 Cm 6 Cm Ii 2 Cm 2 Cm 5 Cm Iii 15 Cm 2cm 25 Cm