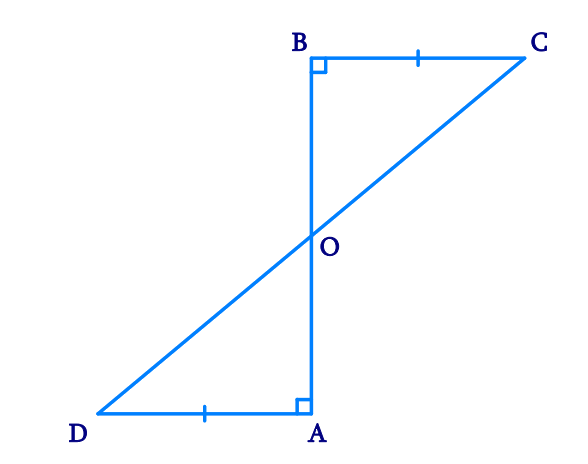
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

Solution:

Given: AD ⊥ AB, BC ⊥ AB, and AD = BC

To Prove: CD bisects AB or OA = OB

We can show that the two triangles OBC and OAD are congruent by using AAS congruency rule and then we can say corresponding parts of congruent triangles will be equal.

Consider two triangles △ BOC and △ AOD,

In △ BOC and △ AOD,

∠BOC = ∠AOD (Vertically opposite angles)

∠CBO = ∠DAO (Each 90º, since AD and BC are ⊥ to AB)

BC = AD (Given)

∴ △BOC ≅ △AOD (AAS congruence rule)

∴ BO = AO (By CPCT)

Thus, CD bisects AB and O is the mid-point of AB.

☛ Check: Class 9 Maths NCERT Solutions Chapter 7

Video Solution:

AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.1 Question 3

Summary:

If AD and BC are equal perpendiculars to a line segment AB, then from the given figure we can say that CD bisects AB and O is the midpoint of AB.

☛ Related Questions:

• Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:i) ΔAPB ≅ ΔAQBii) BP = BQ or B is equidistant from the arms of ∠A
• In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
• AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that Show that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). i) ΔDAP ≅ ΔEBP ii) AD = BE
• In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:i) ΔAMC ≅ ΔBMDii) ∠DBC is a right angle.iii) ΔDBC ≅ ΔACBiv) CM = 1/2 AB