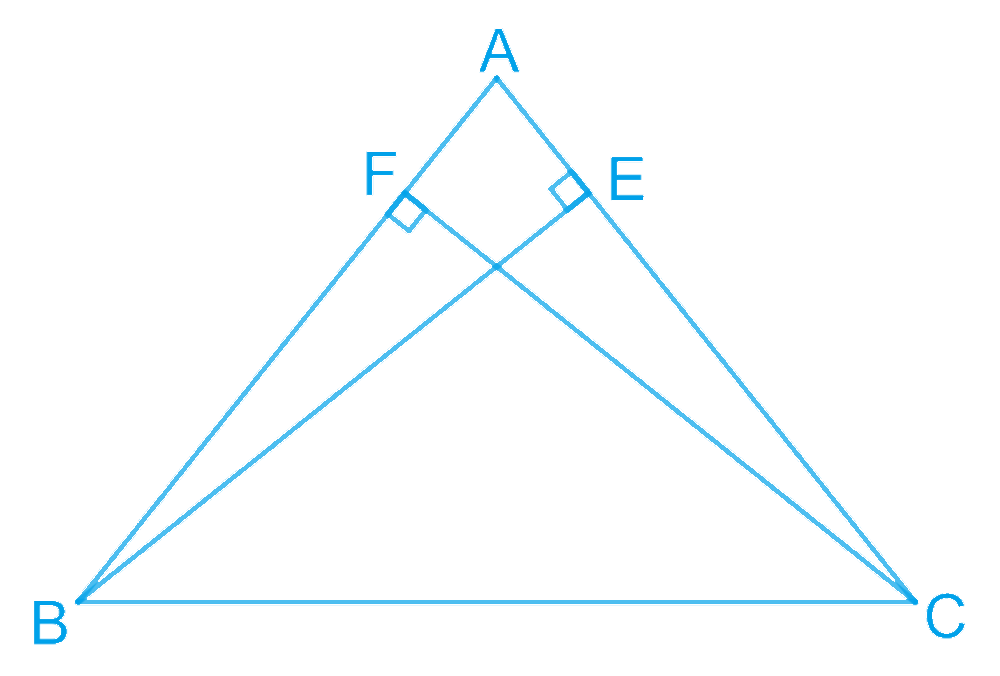
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE ≅ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Solution:

(i) In ΔABE and ΔACF,

∠AEB = ∠AFC (Each 90°)

∠A = ∠A (Common angle)

BE = CF (Given)

∴ ΔABE ≅ ΔACF (By AAS congruence rule)

(ii) We have proved above that ΔABE ≅ ΔACF

∴ AB = AC (By CPCT)

Hence, ΔABC is an isosceles triangle.

☛ Check: NCERT Solutions for Class 9 Maths Chapter 7

Video Solution:

ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that (i) ΔABE ≅ ΔACF (ii) AB = AC, i.e., ABC is an isosceles triangle.

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.2 Question 4

Summary:

If ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal, then ΔABE ≅ ΔACF using AAS congruency and AB = AC i.e., ABC is an isosceles triangle.

☛ Related Questions:

• ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ABD = ∠ACD.
• ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a right angle.
• ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
• Show that the angles of an equilateral triangle are 60° each.