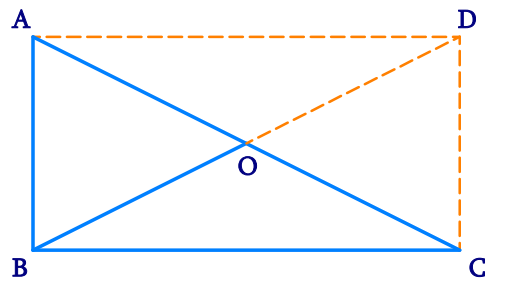
ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).

Solution:

ABCD is a rectangle as opposite sides are equal and parallel to each other and all the interior angles measure 90°.

Thus, AD ∥ BC, AB ∥ DC and AD = BC, AB = DC

In a rectangle, diagonals are of equal length and they bisect each other.

Hence, AO = OC = BO = OD

Thus, two right triangles make a rectangle where O is an equidistant point from A, B, C, and D because O is the mid-point of the two diagonals of the rectangle ABCD.

Therefore, O is equidistant from A, B, C, and D.

☛ Check: NCERT Solutions for Class 8 Maths Chapter 3

Video Solution:

ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C

NCERT Solutions for Class 8 Maths Chapter 3 Exercise 3.4 Question 6

Summary:

ABC is a right-angled triangle and O is the midpoint of the side opposite to the right angle. O is the equidistant point from A, B, C, and D because O is the mid-point of the two diagonals of the rectangle ABCD.

☛ Related Questions:

• State whether True or False. (a) All rectangles are squares (b) All rhombuses are parallelograms (c) All squares are rhombuses and also rectangles (d) All squares are not parallelograms. (e) All kites are rhombuses. (f) All rhombuses are kites.  (g) All parallelograms are trapeziums. (h) All squares are trapeziums.
• Identify all the quadrilaterals that have: (a) four sides of equal length (b) four right angles
• Explain how a square is. (i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
• Name the quadrilaterals whose diagonals. (i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal (i) parallelogram, rhombus, rectangle, and square bisect each other. (ii) square and rhombus are perpendicular bisectors of each other. (iii) rectangle and square are equal.