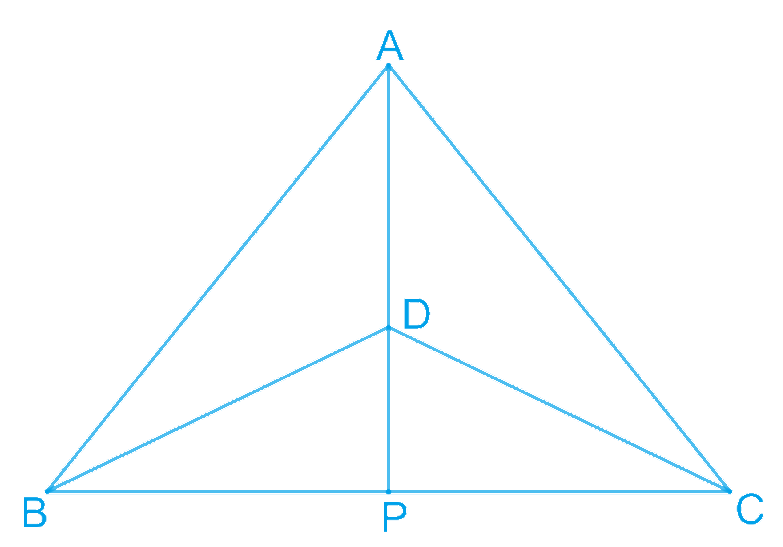
Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.

Solution:

Given: Δ ABC and Δ DBC are isosceles triangles.

(i) In ΔABD and ΔACD,

AB = AC (Equal sides of isosceles ΔABC)

BD = CD (Equal sides of isosceles ΔDBC)

AD = AD (Common)

ΔABD ≅ ΔACD (By SSS congruence rule)

By CPCT, we get

∠BAD = ∠CAD

∠BAP = ∠CAP…. (1)

∠ADB = ∠ADC…. (2)

(ii) In ΔABP and ΔACP,

AB = AC (Given)

∠BAP = ∠CAP [From equation (1)]

AP = AP (Common)

∴ ΔABP ≅ ΔACP (By SAS congruence rule)

∴ BP = CP (By CPCT)…. (3)

(iii) From Equation (1) we know that ∠BAP = ∠CAP

Hence, AP is the angle bisector of ∠A.

From equation (2), we know that ∠ADB = ∠ADC

⇒ 180° - ∠ADB = 180° - ∠ADC

⇒ ∠BDP = ∠CDP .... (4)

Hence, AP is the bisector of ∠D.

(iv) In ΔBDP and ΔCDP,

DP = DP (Common side)

∠BDP = ∠CDP (Using (4))

DB = DC (Equal sides of isosceles ΔDBC)

∴ ΔBDP ≅ ΔCDP (By SAS conguence rule)

∴ ∠BPD = ∠CPD (By CPCT)…. (5)

∠BPD + ∠CPD = 180° (Linear pair angles)

∠BPD + ∠BPD = 180° [From Equation (5)]

∠BPD = 90°… (6)

Also, BP = CP [From equation (3)]

Thus, AP is the perpendicular bisector of BC.

☛ Check: NCERT Solutions Class 9 Maths Chapter 7

---

Video Solution:

Δ ABC and Δ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD ≅ ΔACD (ii) ΔABP ≅ ΔACP (iii) AP bisects ∠A as well as ∠D iv) AP is the perpendicular bisector of BC.

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.3 Question 1

Summary:

If ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC, AD is extended to intersect BC at P, then ΔABD ≅ Δ ACD, ΔABP ≅ ΔACP, AP bisects ∠A as well as ∠D, and AP is the perpendicular bisector of BC. 

---

☛ Related Questions:

• AD is an altitude of an isosceles triangle ABC in which AB = AC.Show that i) AD bisects BC ii) AD bisects ∠A.
• Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:(i) Δ ABM ≅ Δ PQN(ii) Δ ABC ≅ Δ PQR
• BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
• ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.