A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower

Solution:

The ratio of any two corresponding sides in two equiangular triangles is always the same.

Let's visualise the situation according to the given question.

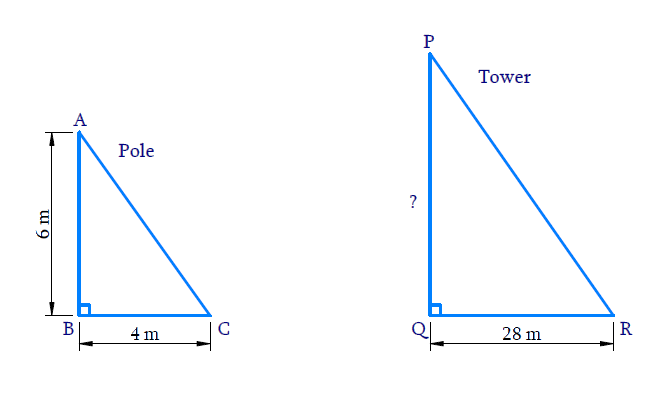
AB is the pole = 6 m

BC is the shadow of pole AB = 4 m

PQ is the tower = ?

QR is the shadow of the tower PQ = 28 m

In ΔABC and ΔPQR

∠ABC = ∠PQR = 90º (The objects and shadows are perpendicular to each other)

∠BAC = ∠QPR  (Sunray falls on the pole and tower at the same angle, at the same time)

⇒ ΔABC ∼ ΔPQR (AA criterion)

The ratio of any two corresponding sides in two equiangular triangles is always the same.

⇒ AB/BC = PQ/QR

⇒ 6/4 = PQ / 28

⇒ PQ = (6 × 28 )/4

⇒ PQ = 42 m

Hence, the height of the tower is 42 m.

☛ Check: NCERT Solutions for Class 10 Maths Chapter 6

Video Solution:

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower
 

NCERT Class 10 Maths Chapter 6 Exercise 6.3 Question 15

Summary:

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Hence the height of the tower is 42 m.

☛ Related Questions:

• In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that: (i) ΔABC ~ ΔAMP (ii) CA/PA = BC/MP.
• CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that: (i) CD/GH =AC/FG (ii) ∆DCB ~ ∆HGE (iii) ∆DCA ~ ∆HGF
• In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥AC, prove that ∆ ABD ~ ∆ ECF.
• Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR.