

A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel
Solution:
Given, a transversal intersects two parallel lines
We have to prove that the bisectors of any pair of corresponding angles formed are parallel.
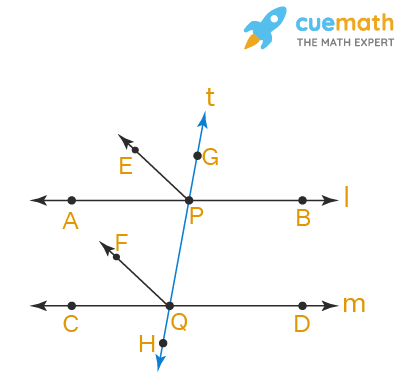
Consider two parallel lines AB and CD cut by a transversal HG
We know that if a transversal intersects two parallel lines, then corresponding angles are equal and conversely.
The corresponding angles are ∠APG and ∠CQP
So, ∠APG = ∠CQP --------------------- (1)
EP is the bisector of ∠APG
∠APE = ∠EPG
∠APG = ∠APE + ∠EPG
∠APG = ∠EPG + ∠EPG
∠APG = 2∠EPG
∠EPG = 1/2 ∠APG ------------------- (2)
FQ is the bisector of ∠CQP
∠CQF = ∠FQP
∠CQP = ∠CQF + ∠FQP
∠CQP = ∠FQP + ∠FQP
∠CQP = 2∠FQP
∠FQP = 1/2 ∠CQP ------------------ (3)
Dividing equation (1) by 2 on both sides,
1/2 ∠APG = 1/2 ∠CQP
From (2) and (3),
∠EPG = ∠FQP
From the figure, we observe that ∠EPG and ∠FQP are the corresponding angles on the transversal HG
Therefore, EP is parallel to FQ
✦ Try This: In the figure given above, l∥m. Find the values of x,y and z.

☛ Also Check: NCERT Solutions for Class 9 Maths Chapter 6
NCERT Exemplar Class 9 Maths Exercise 6.4 Problem 3
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel
Summary:
An angle bisector or the bisector of an angle is a ray that divides an angle into two equal parts. A transversal intersects two parallel lines. It is proven that the bisectors of any pair of corresponding angles so formed are parallel
☛ Related Questions:
visual curriculum