A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16)

Solution:

From the above figure, we can see that the conical depressions do not contain wood. Since the dimensions of all 4 conical depressions are the same, their volumes will also be identical.

Volume of wood in the entire pen stand = Volume of the wooden cuboid - 4 × Volume of the conical depression

We will find the volume of the solid by using formulae;

Volume of the cuboid = lbh, where l, b, and h are the length, breadth, and height of the cuboid respectively.

Volume of the cone = 1/3 πr²h₁, where r and h₁ are the radius and height of the cone respectively.

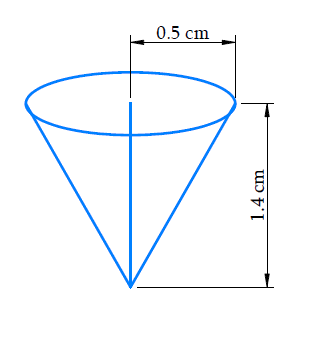
Depth of each conical depression, h₁ = 1.4 cm

Radius of each conical depression, r = 0.5 cm

Dimensions of the cuboid are 15 cm × 10 cm × 3.5 cm

Volume of wood in the entire pen stand = volume of the wooden cuboid - 4 × volume of the conical depression

= l × b × h - 4 × 1/3 πr²h₁

= (15 cm × 10 cm × 3.5 cm) - (4 × 1/3 × 22/7 × 0.5 cm × 0.5 cm × 1.4 cm)

= 525 cm³ - 1.47 cm³

= 523.53 cm³

The volume of wood in the entire stand is 523.53 cm³.

☛ Check: NCERT Solutions Class 10 Maths Chapter 13

Video Solution:

A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16).

NCERT Solutions Class 10 Maths  Chapter 13 Exercise 13.2 Question 4 

Summary:

A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. The volume of wood in the entire stand is 523.53 cm³.

☛ Related Questions:

• A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
• A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3of iron has approximately 8 g mass. (Use π = 3.14)
• A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
• A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.