Natural Log Formula

Logarithms are nothing but an alternative way of writing the exponents. Understanding logarithms is not so difficult. It is sufficient to know that a logarithmic equation is just an alternative way of expressing an exponential equation. So let's define the natural log formula using an exponent. If e^x = a, then \(\log_{e} A = x\) and vice-versa. We read \(\log_{e} A = x\) as 'Logarithm of a to the base e is equal to x'. Logarithms to the base e are called natural logarithms. 

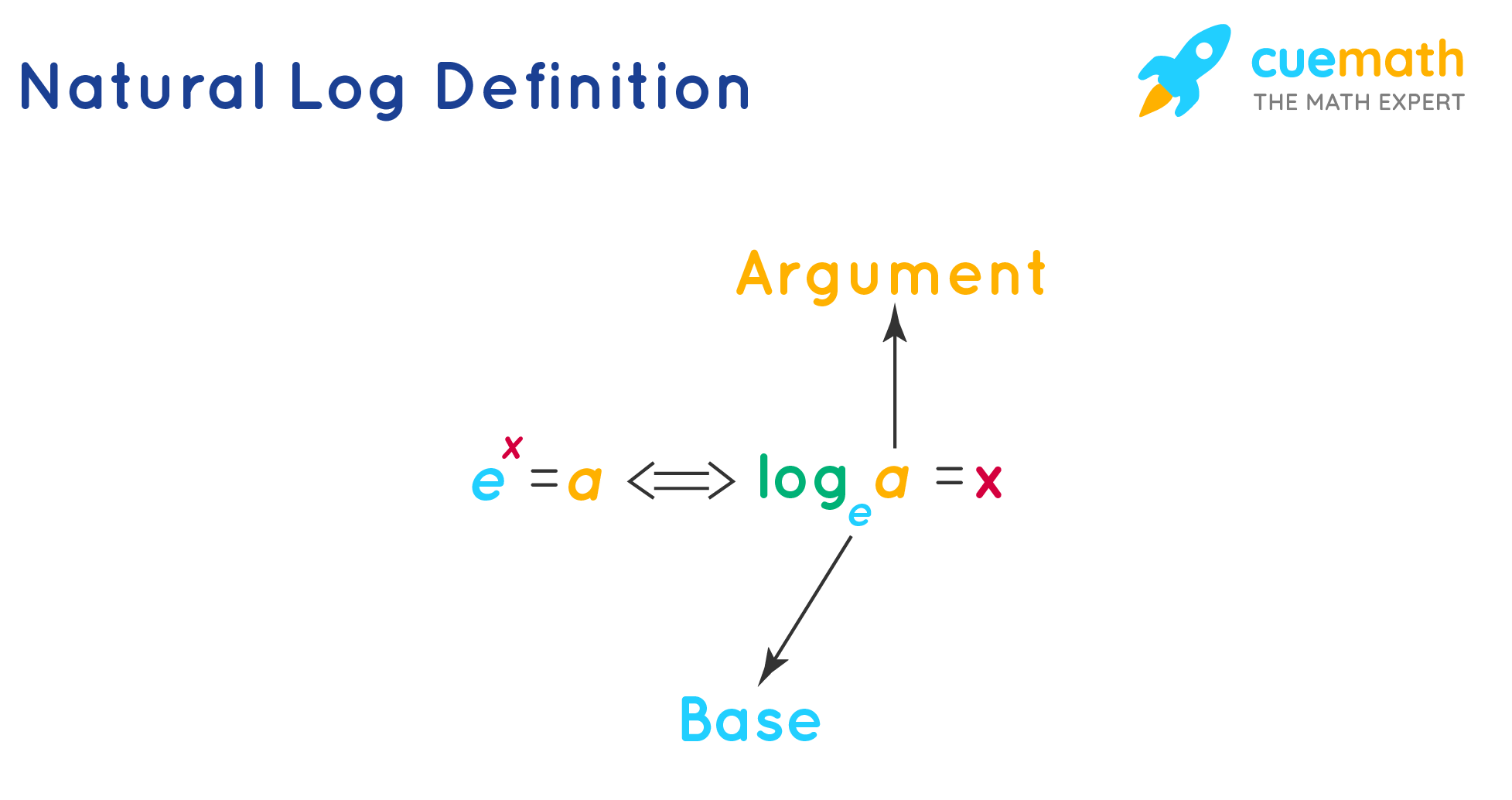
Let us learn the natural log formula with a few solved examples.

What is the Natural Log Formula?

We will show 4 natural log formulas. Here are the formulas of the natural log. 

Product Rule: The logarithm of a product of two numbers is the sum of the logarithms of the individual numbers.

\[\log_e (mn) = \log_e m + \log_e n\]

Quotient Rule: The logarithm of a quotient of two numbers is the difference between the logarithms of the individual numbers.

\[\log_e \left( \dfrac{m}{n} \right) = \log_e m - \log_e n\]

Power Rule: The exponent of the argument of a logarithm can be brought in front of the logarithm.

\[\log_e a^m = m \log_e a\]

Change of Base Rule: The base of a logarithm can be changed using this property.

\[\log _{e} a=\dfrac{\log _{c} a}{\log _{c} e}​\]

OR

\[\log _{e} a \, \cdot\, \log _{c} e=\log _{c} a\]

Let's take a quick look at a couple of examples to understand the natural log formula better.

Examples Using Natural Log Formula

Example 1: Find the integer value of x using natural log formulas: e^3x = 9.

Solution:

e^3x = 9
ln (e^3x) = ln(9)
3x = ln(9)
x = ln(9)/3

Example 2: Simplify: \(6 \ln _{e}(y)+2 \ln _{e}(4 y)-\ln _{e}\left(8 y^{6}\right)\)

Solution:

\begin{align}&6 \ln _{e}(y)+2 \ln _{e}(4 y)-\ln _{e}\left(8 y^{6}\right)\\&=\ln _{e}\left(y^{6}\right)+\ln _{e}\left( (4 y)^{2}\right)-\ln _{e}\left(8 y^{6}\right) \\ &=\ln _{e}\left(y^{6}\right)+\ln _{e}\left(16 y^{2}\right)-\ln _{e}\left(8 y^{6}\right) \\[0.3cm] &=\ln _{e}\left(y^{6} \cdot 16 y^{2}\right)-\ln _{e}\left(8 y^{6}\right) \\[0.3cm] &=\ln _{e}\left(16 y^{8}\right)-\ln _{e}\left(8 y^{6}\right) \\[0.3cm] &=\ln _{e}\left(\frac{16 y^{8}}{8 y^{6}}\right)\\[0.3cm] &= \ln _{e}\left(2 y^{2}\right) \end{align}