Perimeter of a Sector
The perimeter of a sector is the total boundary of a sector. A sector is a part of a circle that is formed with two radii and an arc that joins them. Therefore, the perimeter of a sector of a circle can be calculated by adding the length of two radii and the length of the arc which forms the sector. Let us learn more about the perimeter of a sector of a circle in this article.
| 1. | What is the Perimeter of a Sector? |
| 2. | Perimeter of Sector Formula |
| 3. | Perimeter of Sector of a Circle |
| 4. | Perimeter of a Sector using Area |
| 5. | FAQs on Perimeter of a Sector |
What is the Perimeter of a Sector?
The perimeter of a sector is the length of the boundary of the sector of a circle. This boundary includes the length of two radii and the arc that forms the particular sector. Observe the figure given below to understand what the perimeter of a sector means.
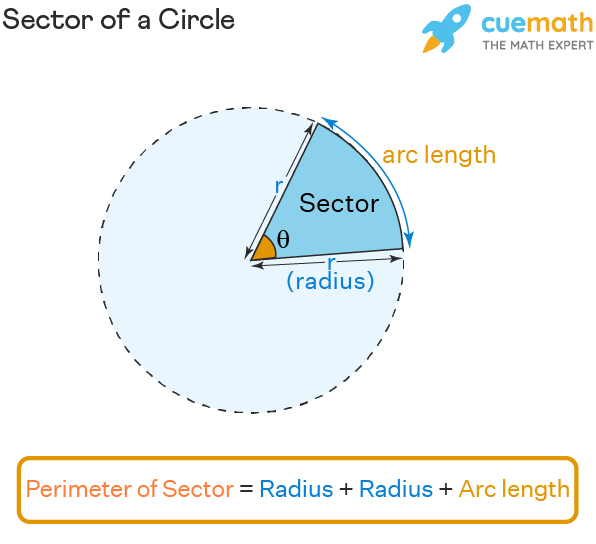
Perimeter of Sector Formula
The formula for perimeter of sector can be understood by using the figure given above which shows that the perimeter of a sector can be calculated if we know the arc length and the radius of the circle. The formula is Perimeter of sector = Radius + Radius + Arc length. Here, if the arc length is not given, it can be calculated using the formula, Arc length = r × θ, where 'r' is the radius and θ is the angle of the sector in radians. Let us read about this in detail in the following sections.
Perimeter of Sector of a Circle
The perimeter of a sector of a circle includes the length of the two radii and the arc length that forms the sector. While we can easily get the length of the radius of the sector, the arc length needs to be calculated using a formula. Arc length = r × θ, where 'r' is the radius and θ is the angle of the sector in radians. It should be noted that this angle θ needs to be in the form of radians. After the arc length is calculated, the perimeter of the sector can be calculated by finding the sum of the 2 radii and the arc length.
How to find the Perimeter of a Sector?
The perimeter of a sector can be calculated once we know the radius and the arc length. If the angle of the sector is given in degrees, we need to convert it into radians and then the arc length can be calculated to get the perimeter of the sector. Let us understand this with an example.
Example: Find the perimeter of a sector of a circle whose radius is 11 units and the angle of the sector subtended by the arc is 10°.
Solution: The length of the radius = 11 units, Angle of the sector =10° which needs to be converted to radians. Let us follow the steps given below to find the perimeter of the sector.
- In order to convert an angle from degree to radians, we use the formula, Radians = Degrees × π /180
- This means we need to multiply the given value of degrees by π /180. This will make it (10 × π) /180 = π /18
- Now, we can find the arc length using the formula, Arc length = r × θ; (where r = radius = 11 units, θ = angle of the sector in radians = π /18)
- Arc length = 11 × π /18, Arc length = (11 × 3.14)/18 = 1.92 units
- Now, that we know the arc length, we can find the perimeter of the sector by adding the values because we know that Arc length = 1.92 units, Radius = 11 units
- Perimeter of sector = Radius + Radius + Arc length, Perimeter of sector = (2 × radius) + Arc length, Perimeter of sector = (2 × 11) + 1.92 ⇒ 22 + 1.92 = 23.92 units.
- Therefore, the perimeter of the sector is 23.92 units.
Perimeter of a Sector using Area
The perimeter of a sector can be calculated if the area of the sector is given. We know that the area of a sector can be calculated using the following formulas,
- Area of a Sector of Circle = (θ/360º) × πr2, where, θ is the sector angle subtended by the arc at the center, in degrees, and 'r' is the radius of the circle.
- Area of a Sector of Circle = 1/2 × r2θ, where, θ is the sector angle subtended by the arc at the center, in radians, and 'r' is the radius of the circle.
Therefore, if the area of the sector and the radius is given, then we can find the angle of the sector using the following steps.
- Step 1: We can find the angle of the sector using the appropriate formula for the area of the sector (given above).
- Step 2: Once the angle is known, the arc length can be calculated using the formula, Arc length = r × θ; (where r = radius and θ = angle of the sector in radians)
- Step 3: Once the Arc length is calculated, the perimeter of the sector can be calculated using the formula, Perimeter of sector = Radius + Radius + Arc length
Let us understand this with the help of an example.
Example: Find the perimeter of a sector whose area is 324 square units and the radius is 27 units.
Solution: Let us find the perimeter of the sector using the following steps:
- We know that, Area of a Sector of Circle = 1/2 × r2θ, where, θ is the sector angle subtended by the arc at the center, in radians, and 'r' is the radius of the circle.
- After substituting the value of the area of the sector = 324, and radius = 27 units, we can calculate the angle of the sector.
- This will be, Area of a Sector of Circle = 1/2 × r2θ ⇒ 324 = 1/2 × 272 × θ. After solving this equation, we get the value of θ = 0.89
- Now, we can find the arc length using the formula, Arc length = r × θ ⇒ 27 × 0.89 = 24 units.
- Finally, the perimeter of the sector can be calculated because we know that Arc length = 24 units, and radius = 27 units. So, after substituting these values in the formula, Perimeter of sector = Radius + Radius + Arc length, we get, Perimeter of sector = 27 + 27 + 24 = 78 units.
☛ Related Topics
Perimeter of a Sector Examples
-
Example 1: Find the perimeter of a sector of a circle of radius 5.2 units and the arc length is 2 units.
Solution: Radius of the sector of the circle = 5.2 units, Arc length = 2 units.
We can find the perimeter of the sector using the formula,
Perimeter of sector = Radius + Radius + Arc length
Perimeter of sector = 5.2 + 5.2 + 2 = 12.4 units
-
Example 2: Find the perimeter of a sector of a circle whose angle is 90° and radius is 7 cm.
Solution:
Radius of the sector of the circle = 7 cm, angle of the sector = 90°
We need to convert the angle from degrees to radians using the formula, Radians = Degrees × π /180
Radians = 90° × π /180 = π/2
Now, we can find the arc length using the formula, Arc length = r × θ; (where r = radius = 7, and θ = angle of the sector in radians = π/2)
Arc length = r × θ
Arc length = 7 × π/2 = (7 × 3.14)/2 = 10.99 ⇒ 11 cm
Now, we can find the perimeter of the sector using the formula,
Perimeter of sector = Radius + Radius + Arc length
Perimeter of sector = 7 + 7 + 11 = 25 cm
-
Example 3: Find the perimeter of a sector of a circle with central angle θ = π/2 and radius = 8 ft.
Solution:
Radius of the sector of the circle = 8 ft., angle of the sector θ = π/2
So, we can find the arc length using the formula, Arc length = r × θ; (where r = radius = 8, and θ = angle of the sector in radians = π/2)
Arc length = r × θ
Arc length = 8 × π/2 = (8 × 3.14)/2 = 12.56 ft.
Now, we can find the perimeter of the sector using the formula,
Perimeter of sector = Radius + Radius + Arc length
Perimeter of sector = 8 + 8 + 12.56 = 28.56 ft.

FAQs on Perimeter of a Sector
What is the Perimeter of a Sector?
The perimeter of a sector of a circle is the total length of its boundary which includes 2 radii and the arc length that forms the sector. It can be calculated if the length of the arc and the radius is known.
What is the Formula for Perimeter of Sector?
The formula that is used to find the perimeter of a sector is, Perimeter of sector = Radius + Radius + Arc length. Here, if the arc length is not known, it can be calculated with the formula, Arc length = r × θ; (where r = radius and θ = angle of the sector in radians). If the angle of the sector is not given in radians, it can be converted from degrees to radians using the formula, Radians = Degrees × π /180
How to Find the Perimeter of a Sector of a Circle?
The perimeter of a sector can be calculated using the following steps. Let us find the perimeter of a sector of a circle whose radius is 9 units and the angle subtended by the arc is 10°.
Solution: The length of the radius = 9 units. The angle of the sector = 10° which needs to be converted to radians. Let us follow the steps given below to find the perimeter of the sector.
- In order to convert an angle from degree to radians, we use the formula, Radians = Degrees × π /180
- This means we need to multiply the given value of degrees by π /180. This will be (10 × π) /180 = π /18
- Now, we can find the arc length using the formula, Arc length = r × θ; (where r = radius = 9 units, θ = angle of the sector in radians = π /18)
- Arc length = 9 × π /18, Arc length = (9 × 3.14)/18 = 1.57 units
- Now, that we know the arc length, we can find the perimeter of the sector by adding the values because we know that Arc length = 1.57 units, Radius = 9 units
- Perimeter of sector = Radius + Radius + Arc length, Perimeter of sector = (2 × radius) + Arc length, Perimeter of sector = (2 × 9) + 1.57, ⇒ 18 + 1.57 = 19.57 units.
- Therefore, the perimeter of the sector is 19.57 units.
What is the Perimeter of a Sector with Radius 10.5 cm and Sector Angle 60°?
The perimeter of sector with radius 10.5 cm and sector angle 60° can be calculated using the following steps.
- First of all, we need to convert the angle of the sector from degrees to radians. Given, radius of the sector = 10.5 cm, Angle of the sector = 60°. So, the value of the angle in radians can be calculated using the formula, Radians = Degrees × π /180 ⇒ Radians = 60 × π /180 = π/3
- Now, the arc length can be calculated using the formula, Arc length = r × θ; (where r = radius = 10.5 cm, θ = angle of the sector in radians = π /3). So Arc length = 10.5 × π /3 = 10.99 = 11 cm
- Now, the perimeter of the sector can be calculated using the formula, Perimeter of sector = Radius + Radius + Arc length, Perimeter of sector = 10.5 + 10.5 + 11 ⇒ 32 cm
How to find the Perimeter of Sector using Arc Length Formula?
The perimeter of a sector can be calculated if the arc length is given because the formula for the perimeter of a sector is, Perimeter of sector = Radius + Radius + Arc length. Now, if the arc length is not given we can calculate it using the arc length formula, Arc length = r × θ; (where r = radius of the sector, and θ = angle of the sector in radians). Once the arc length is known, the perimeter of the sector can be calculated.
How to Find the Perimeter of a Sector of a Circle with Radius?
The perimeter of a sector of a circle can be calculated if the radius and the arc length of the sector is given. The formula which is used to find the perimeter of a sector using radius is, Perimeter of sector = Radius + Radius + Arc length.
What is the Circumference of a Sector?
The circumference of a sector is the total length of the boundary of the sector. In other words, it is the perimeter of the sector of a circle. This circumference of a sector can be calculated if the radius and the arc length is known. The formula which is used to find the perimeter of a sector using radius is, Perimeter of sector = Radius + Radius + Arc length.
visual curriculum
