Base Area of a Triangular Prism
In this section, we will discuss the base area of a triangular prism along with solved examples. The base area of a triangular prism is the area of the triangle of the prism. Let us start with the pre-required knowledge to understand the topic base area of a triangular prism. Recall that a prism is a solid which has identical polygon ends (bases), flat parallelogram sides, and has the same cross-section all along its length.
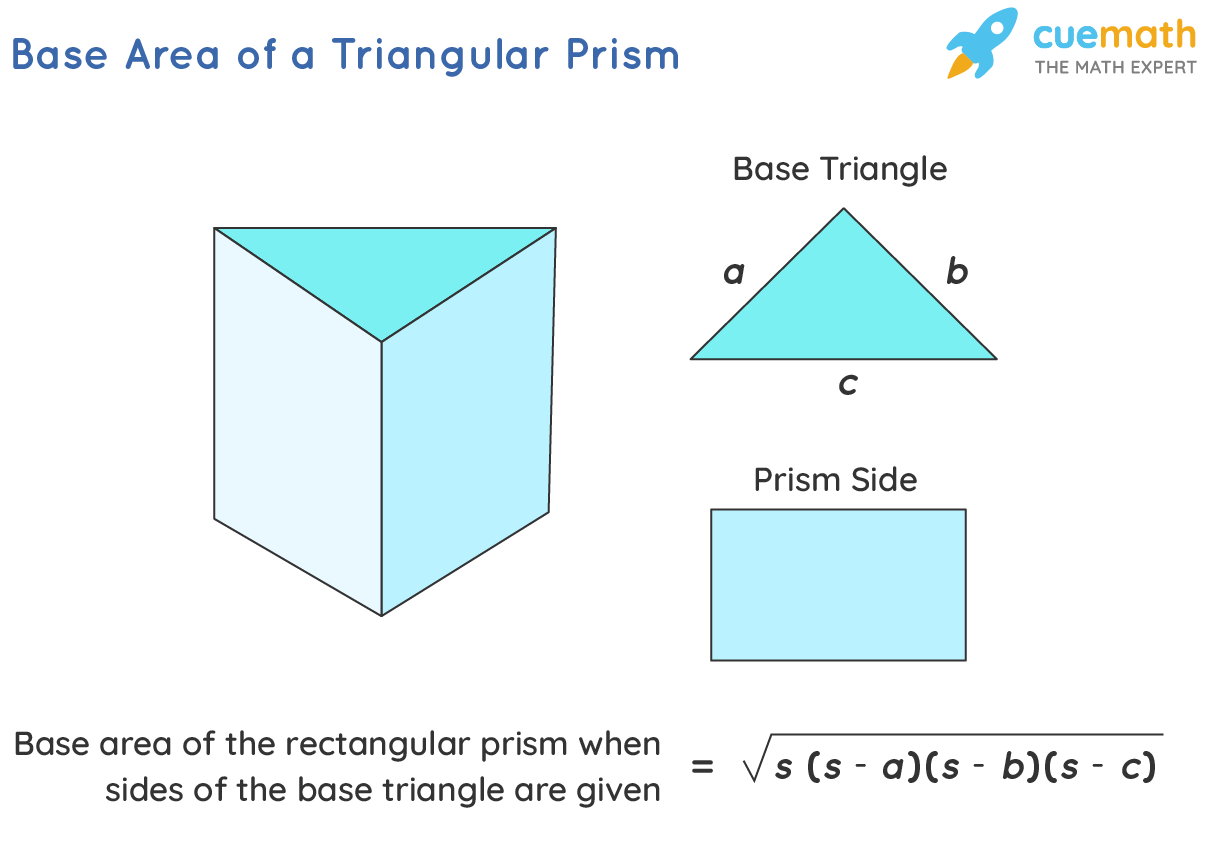
A prism having three faces as rectangles and two triangles as its bases (one triangle acts as the top) is called a triangular prism. It's a three-sided prism where the base and top are equal triangles and the remaining 3 sides are rectangles. Both of the triangles are parallel and congruent to each other. The rectangles need not be congruent with each other.
| 1. | What Is Base Area of a Triangular Prism? |
| 2. | Base Area of a Triangular Prism Using Sides |
| 3. | Base Area of a Triangular Prism Formula with Height and Base |
| 4. | FAQs on Base Area of Triangular Prism |
What Is Base Area of a Triangular Prism?
The base area of a triangular prism is defined as the total area covered by the bases of a triangular prism. The base area of the triangular prism is expressed in square units. The area of the base of a triangular prism can be calculated using different formulas, depending upon the known parameters and type of triangle in the base. Let us understand these formulas in the following sections.
Base Area of a Triangular Prism if the Sides of Its Triangle Are Given
For a triangular prism, if the length of the sides of the triangular base of the prism is given, then its base area can be given by:
Base area of a triangular prism = Area of the base triangle
Using Heron's formula for the area of a triangle we get,
Base area of a triangular prism = √[s(s − a)(s − b)(s − c)]
where,
- a, b, c are the lengths of the sides of the base triangle, and,
- s is its semi-perimeter and is equal to (a + b + c)/2
Example: How to find the base area of a triangular prism given the length of the sides of the base triangle: a = 20 units, b = 10 units, and c = 20 units?
Semi-perimeter (s) = (20 + 10 + 20)/2 = 25 units
Base area of the given triangular prism = √[s(s − a)(s − b)(s − c)] = √[25(25 − 20)(25 − 10)(25 − 20)] = √[25(5)(15)(5)] = 25√15 square units.
Base Area of a Triangular Prism Formula if the Base and Height of the Triangle Are Given
For a triangular prism, if the length of the base and height of the base triangle is given, then its base area can be given by,
Base area of a triangular prism = Area of the base triangle
Base area of a triangular prism = (1/2) × b × h
where,
- b is the length of the base of the triangle, and,
- h is the height of the triangle

Example: How to find the base area of a triangular prism given the height of the triangle h = 10 units and base b = 20 units?
Solution: Base area of the given triangular prism = (1/2) × b × h = (1/2) × 20 × 10 = 100 square units
Important Notes on Base Area of a Triangular Prism
- The base area of a triangular prism can be calculated when three sides of the base triangle are given.
- The base area of a triangular prism can be calculated when the base length and height of the base triangle are given.
Related Topics on Base Area of a Triangular Prism
Solved Examples on Base Area of a Triangular Prism
-
Example 1: Find the base area of the triangular prism whose base triangle has the height = 60 units and base length = 40 units.
Solution:
Height of the triangular prism = 60 units
Base length of the triangular prism = 40 units
Base area of the given triangular prism = 1/2 × Base length × Height of the base triangle = 1/2 × 60 × 40 = 120 square units
Answer: Base area of the given triangular prism = 120 square units
-
Example 2: Find the base area of the triangular prism whose base triangle has the length of the sides a = 3 units, b = 4 units, and c = 5 units.
Solution:
Length of the sides a = 3 units, b = 4 units, and c = 5 units.
Semi-perimeter of the base triangle (s) = (3 + 4 + 5)/2 = 6 units
Base area of the given triangular prism = √[s(s−a)(s−b)(s−c)]s = √[6(6−3)(6−4)(6−5)] = √[6(3)(2)(1)] = 6 square units
Answer: Base area of the given triangular prism = 6 square units.

FAQs on the Base Area of a Triangular Prism
What Is Base Area Triangular Prism?
The base area of a triangular prism is defined as the region or area covered by the bases of a triangular prism. A triangular prism has 2 triangle-shaped bases.
How to Calculate the Base Area of a Triangular Prism?
The base area of a triangular prism can be calculated as,
- Note down the dimensions of the triangle in bases.
- Apply the formulas to calculate the area of the base triangle and multiply it by 2.
- Express the result with a suitable unit.
What Are the Formulas to Find Base Area of a Triangular Prism?
The formulas that can be used to find the base area of a triangular prism are,
- When base triangle is equilateral, with each side 'a', then area = √3a2/4.
- When base triangle's base 'b' and height 'h' is given, then area = (1/2) bh.
- When base triangle is a right-angled triangle, with two legs 'b' and 'h' then area = (1/2) bh.
- When base triangle is an isosceles triangle with its sides to be 'a', 'a', and 'b' then its area is (b/4) · √(4a2 - b2)
- When base triangle is scalene, with all three sides 'a', 'b', and 'c' are given, then area = √[s(s - a)(s - b)(s - c)], where s = (a + b + c)/2.
- When base triangle's two sides 'a' and 'b' and the included angle 'θ' are given, then area = 1/2 ab sin θ.
What Are the Units Used to Express Base Area of a Triangular Prism?
The units used to express the base area of a triangular prism are in2, m2, cm2, ft2, etc. It is expressed in square units.
How to Calculate the Base Length Using Base Area of a Triangular Prism?
Using the area of triangle formula for the given type of triangle in base, we can calculate the base length by substituting the known values in the formula and solve.
visual curriculum
