Area of a Triangle with 2 Sides and Included Angle
The area of a SAS triangle is the total amount of space it encloses in a 2-dimensional plane. Recall that a SAS triangle is a triangle with two given sides and an included angle between them. The SAS triangle area formula thus helps in calculating the space occupied between the sides of the SAS triangle in a plane. The area of any shape is the number of unit squares that can fit into it. Here, "unit" refers to one (1) and a unit square is a square with a side of 1 unit. In this section, we will discuss the area of a triangle with 2 sides and an included angle (SAS triangle) along with solved examples.
| 1. | Area of a SAS Triangle Formula |
| 2. | Proof on the Area of a SAS triangle |
| 3. | FAQs on Area of a SAS Triangle Formula |
Area of a SAS Triangle Formula
"SAS" which means "Side, Angle, Side", is the property of a triangle whose 2 sides and the angle between these sides is given.
For a given triangle ABC, with two known sides and an included angle between these sides, its area can be calculated using the SAS formula. Consider a,b, and c are the different sides of a triangle.
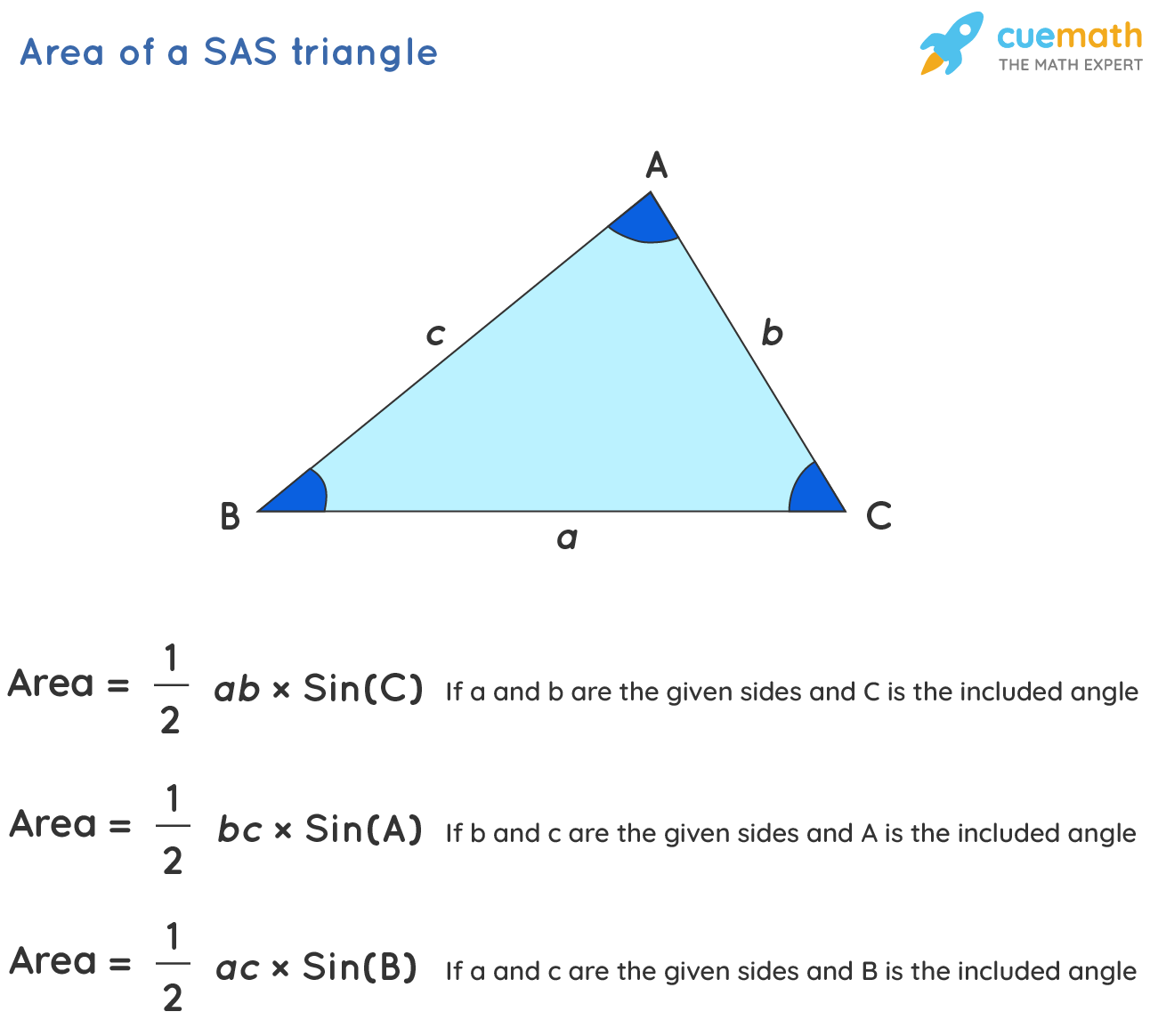
The formula to calculate the area of a triangle using SAS is given as,
- When sides 'b' and 'c' and included angle A is known, the area of the triangle is: 1/2 × bc × sin(A)
- When sides 'b' and 'a' and included angle B is known, the area of the triangle is: 1/2 × ab × sin(C)
- When sides 'a' and 'c' and included angle C is known, the area of the triangle is: 1/2 × ac × sin(B)
Proof on the Area of a SAS Triangle
Consider a,b, and c are the different sides of a triangle.
- When sides 'b' and 'c' and included angle A is known, the area of the triangle is: 1/2 × bc × sin(A)
- When sides 'b' and 'a' and included angle B is known, the area of the triangle is: 1/2 × ab × sin(C)
- When sides 'a' and 'c' and included angle C is known, the area of the triangle is: 1/2 × ac × sin(B)
The above formula can be proved using the following steps:
Given triangle ABC, with two known sides, BC & AC, and an included angle C between these sides. Let us assume the height to be h.
Triangle ACD is a right-angle triangle. Using trigonometry we get,
⇒ sin(C) = h/b
⇒ h = b sin(C)
Height = h = AD = b sin(C)
Base = Length of BC = a (as shown in figure above)
Therefore, area of a triangle ABC = (1/2)(base)(height) = (1/2)(length of BC)(height) = (1/2)(a)(b sin(C))
Solved Examples
-
Example 2
Find the area of the quadrilateral BCED, given that AB = 30 units, AC = 20 units and ∠BAC = 30°. Also, D divides AB in the ratio 1:2 and E is the midpoint of AC.
Solution
Length of AB = 30 units, Length of AC = 20 units
Angle between AB and AC = ∠A = 30°
Area ΔABC = 1/2 × AB × AC × sin(A) = 1/2 × 30 × 20 × sin30º = 150 square units
Given, D divides AB in the ratio of 1:2,
AD = \( \dfrac{1}{1+2}\) AB = 1/3 × 30 = 10 square units
Given, that E is the midpoint of AC, thus AE = AC/2 = 10 units2
Area ΔADE = 1/2 × AD × AE × sin(A) = 1/2 × 10 × 10 × sin30º = 25 square units
Area(BCED) = Area ΔABC - Area ΔADE = 150 - 20 = 125 square units
Answer: Area(BCED) = 125 square units
FAQs on the Area of an SAS Triangle
What is the Area of a Triangle with 2 Sides and Included Angle?
A SAS triangle is a triangle with two given sides and an included angle between them. The area of a triangle with 2 sides and an included angle is the total amount of space it encloses in a 2-dimensional plane which can be calculated using SAS triangle formula.
What Is the Formula for Finding the Area of a SAS Triangle?
Consider a,b, and c are the different sides of a triangle. Thus, the area of a SAS triangle formula is expressed as,
- When sides 'b' and 'c' and included angle A is known, the area of the triangle is: 1/2 × bc × sin(A)
- When sides 'b' and 'a' and included angle B is known, the area of the triangle is: 1/2 × ab × sin(C)
- When sides 'a' and 'c' and included angle C is known, the area of the triangle is: 1/2 × ac × sin(B)
What Is the Meaning of a SAS Triangle?
The angle between the two given sides of the triangle is called the included angle for those sides.
How Can You Find the Area of a SAS Triangle, if S Is the Length of the Equal Sides and θ Is the Angle Between Them?
Since the sides are equal that means it is an isoscele triangle. The area of the given isosceles triangle = 1/2 × s × s × sin(θ) = 1/2 s2 sin(θ) (using SAS triangle area formula).
How Do You Find the Length of the Unknown Side of a SAS Triangle?
Using the cosine law (cosine rule or the cosine formula), the length of the unknown side can be found out. If two sides a and b are given and the included angle C is given, then the unknown side c can be given by c2 = a2 + b2 - 2ab cos(C).
What Is the Perimeter of a SAS Triangle?
Perimeter of a triangle is defined as the total length of the boundary of the triangle, i.e., Perimeter = Sum of all the lengths of the sides of the triangle. For a given triangle ABC, with two known sides, BC & AC, and an included angle C between these sides. Let a be the length of BC, b be the length of AC and c be the length of AB, then its perimeter can be given by, Perimeter = a + b + c. Since c is unknown, it can be given by the cosine formula (cosine rule or the law of cosines) c2 = a2 + b2 - 2ab cos(C). Therefore, perimeter of SAS triangle = \( a + b + \sqrt{a^2 + b^2 - 2ab cos(C)} \)
What Is the Height of a SAS Triangle?
Given triangle ABC, with two known sides, BC & AC, and an included angle C between these sides. Let a be the length of BC, b be the length of AC and c be the length of AB, then its height can be given by, h = a sin(C)