visual curriculum
Table of Contents
| 1. | Introduction |
| 2. | Further Examples |
| 3. | Properties of Number Sets |
| 4. | FAQs |
21 September 2020
Read time: 3 minutes
Introduction
A set is uncountable if it contains so many elements that they cannot be put in one-to-one correspondence with the set of natural numbers. In other words, there is no way that one can count off all elements in the set in such a way that, even though the counting will take forever, you will get to any particular element in a finite amount of time.
Uncountable is in contrast to countably infinite or countable.
The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.
For example, the set of real numbers between 0 and 1 is an uncountable set because no matter what, you'll always have at least one number that is not included in the set. This set does not have a one-to-one correspondence with the set of natural numbers. The proof of this involves creating an infinite list of numbers between 0 and 1 such as this.
|
\(0.12348…\) |
|
\(0.34897…\) |
|
\(0.98789…\) |
|
\(0.43238…\) |
|
\(0.55349...\) |
No matter what kind of list you create, there will always be a number that is not in the list. This is found by using Cantor's diagonal argument, where you create a new number by taking the diagonal components of the list and adding 1 to each. So, you take the first place after the decimal in the first number and add one to it. You get \(1 + 1 = 2.\) Then you take the second place after the decimal in the second number and add 1 to it \((4 + 1 = 5).\) And so on to get your new number:
\(0.25840...\)
(When your number is a \(9,\) you get \(0\) when adding a \(1\))
Further Examples of Uncountable Sets
As we have already seen for countable sets, the concept of countability and cardinality will be explained through examples:
-
Rational Numbers (https://www.cuemath.com/numbers/rational-numbers/)
-
Irrational Numbers (https://www.cuemath.com/numbers/irrational-numbers/)
-
Real Numbers (https://www.cuemath.com/numbers/real-numbers/)
-
Complex Numbers (https://www.cuemath.com/numbers/complex-numbers/)
-
Imaginary Numbers
Properties of the Number Sets
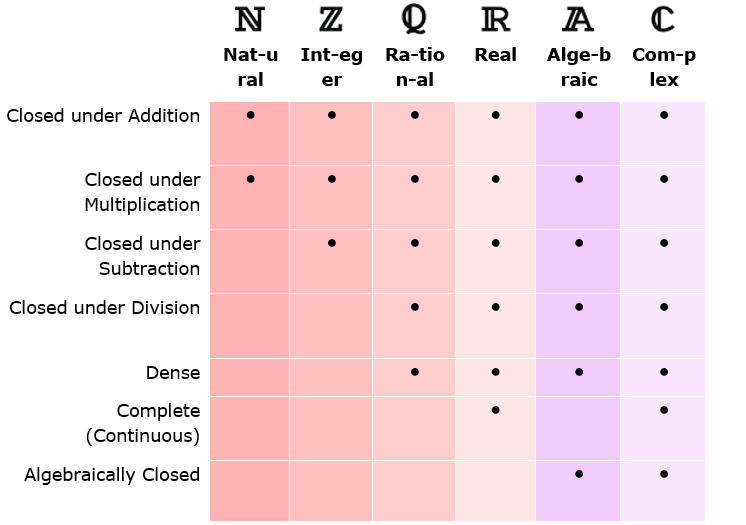
-
Closed under addition (multiplication, subtraction, division) means the sum (product, difference, quotient) of any two numbers in the set is also in the set.
-
Dense: Between any two numbers there is another number in the set.
-
Continuous with no gaps. Every sequence that keeps getting closer together will converge to a limit in the set.
-
Every polynomial with coefficients in the set has a root in the set.
Frequently Asked Questions (FAQs)
What is a countable set?
A countable set is a set of numbers that can have a one to one mapping with the set of natural numbers i.e. are either finite or countably infinite.
What is an uncountable set?
An uncountable set is a set of numbers that don’t have a one to one mapping with the set of natural numbers i.e. they consists of infinite numbers.
What are a few known examples of a countable set?
Examples of countable set include:
- Natural Numbers
- Even Numbers
- Odd Numbers
- Whole Numbers
- Integers
- Positive Integers
- Negative Integers, etc.
What are a few known examples of an uncountable set?
Examples of uncountable set include:
- Rational Numbers
- Irrational Numbers
- Real Numbers
- Complex Numbers
- Imaginary Numbers, etc.
