Lagrange Interpolation Formula

The Lagrange interpolation formula is a way to find a polynomial, called Lagrange polynomial, that takes on certain values at arbitrary points. Lagrange’s interpolation is an Nth degree polynomial approximation to f(x). Let us understand Lagrange interpolation formula using solved examples in the upcoming sections.

What is Lagrange Interpolation Formula?

Given n distinct real values \(x_1, x_2, \ldots, x_n\)​ and n real values \(y_1, y_2, \ldots, y_n\) (not necessarily distinct), there is a unique polynomial P with real coefficients satisfying \(P(x_i) = y_i\) for  i ∈ {1, 2, …, n}, such that deg(P) < n. Lagrange interpolation formula for different order of polynomials is given as,

Lagrange First Order Interpolation Formula

Lagrange's interpolation formula for polynomials of first order can be given as,

 \(f(x) \!\!=\!\! f(x_0)\! +\! (x \!−\! x_0) \!\dfrac{f(x_0) \!−\! f(x_1)}{x_0 − x_1}\)

Use simplified notations \(f_0 \!=\! f(x_0), f_1 \!=\! f(x_1)\), to write:

\(f(x) \!=\! f_0 \!+ \!\dfrac{(x \!−\! x_0)}{(x_1 \!−\! x_0)} (f_1 \!−\! f_0) \\\! =\! f_0 \dfrac{(x_1 \!−\! x_0) \!−\! (x \!−\! x_0)} {(x_1 \!−\! x_0)} \!+\! \dfrac{(x \!−\! x_0)}{(x_1 \!−\! x_0)} f_1 \\ f(x) \!=\! \dfrac{(x \!−\! x_1)}{(x_0 \!−\! x_1)}f_0 \!+\! \dfrac{(x \!−\! x_0)}{(x_1 \!−\! x_0)}f_1\)

Lagrange Second Order Interpolation Formula

Lagrange's interpolation formula for polynomials of second order can be given as,

\(f(x) \!=\! f(x_0) \!+\! (x\! −\! x_0) \!\dfrac{f(x_0)\! −\! f(x_1)}{x_0 \!−\! x_1} \!+\! (x − x_0)(x − x_1) \!\dfrac{f(x_0, x_1) \!−\! f(x_1, x_2)}{x_0 − x_2}\) 

or, \(f(x) \!=\! f_0 \!+\! (x \!−\! x_0) \!\dfrac{f_0 \!−\! f_1}{x_0 \!−\! x_1} \!+\! \dfrac{(x \!−\! x_0)(x\! −\! x_1)}{x_0 \!−\! x_2} \!\left[ \dfrac{f_0 \!−\! f_1}{x_0 \!−\! x_1} − \dfrac{f_1 \!−\! f_2}{ x_1 \!−\! x_2} \right]\)

Collecting terms for \(f_0, f_1 \text{and} f_2\), and after some tedious algebraic manipulation, the second order formula can be written as,

\(f(x) \!=\! \dfrac{(x\! −\! x_1)(x \!− \!x_2)}{(x_0 \!−\! x_1)(x_0 \!− \!x_2)} f_0 \!+\! \dfrac{(x\! − \!x_0)(x \!−\! x_2)}{(x_1 \!−\! x_0)(x_1 \!−\! x_2)}f_1 \!+\! \dfrac{(x \!−\! x_0)(x \!−\! x_1)}{(x_2 \!−\! x_0)(x_2 \!−\! x_1)}f_2\)

Lagrange Interpolation Formula for Nth Degree Polynomial

Lagrange interpolation formula for Nth degree polynomial can be given as,

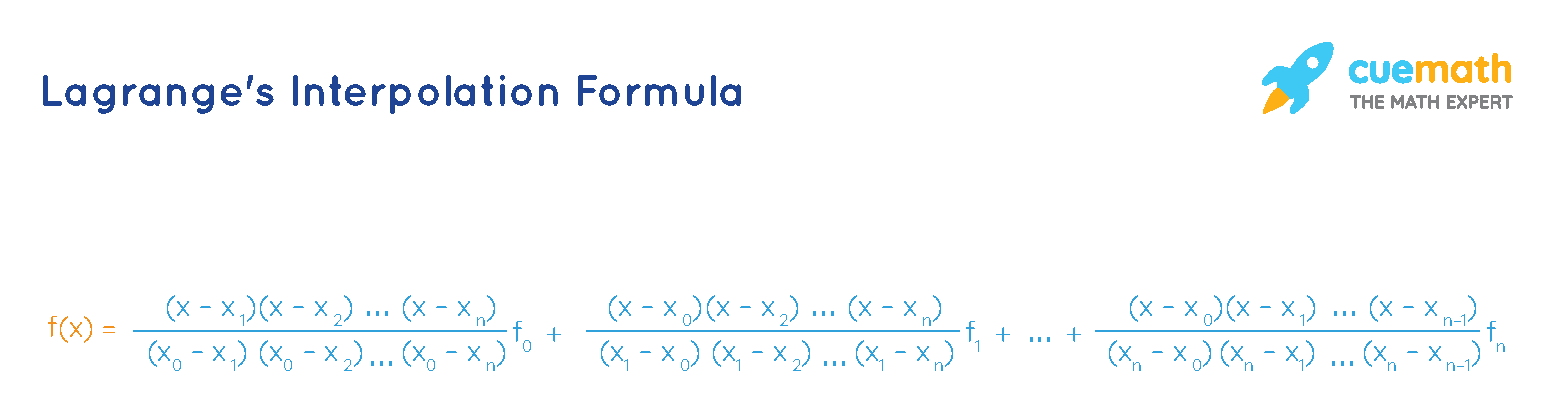
Let us see how to use the Lagrange interpolation formula in the following solved examples section.