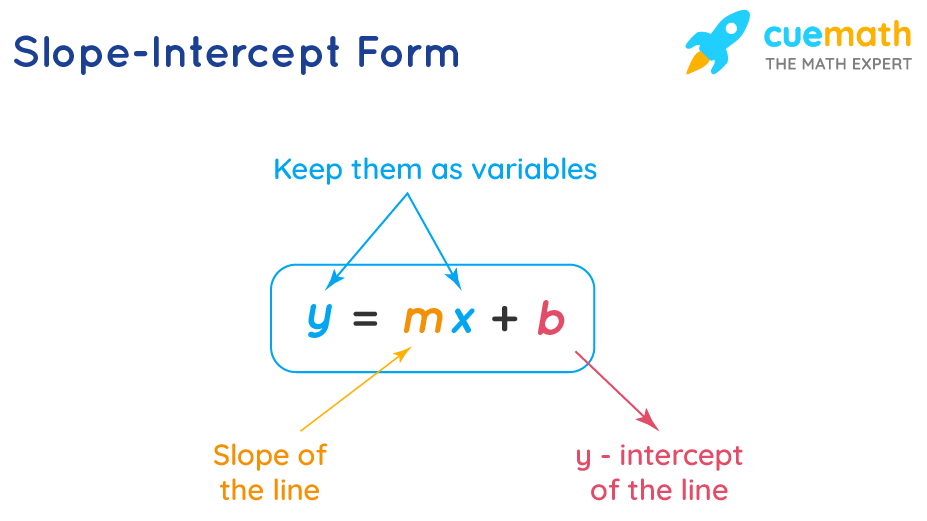
y=mx+b
y = mx + b is the slope intercept form of writing the equation of a straight line. In the equation 'y = mx + b', 'b' is the point, where the line intersects the 'y axis' and 'm' denotes the slope of the line. The slope or gradient of a line describes how steep a line is. It can have either a positive or a negative value. When a standard form of a linear equation is of the form Ax + By = C, where 'x' and 'y' and 'C' are variables and 'A', 'B' are constants, the slope-intercept form is the most preferred way of expressing a straight line due to its simplicity, as it is very easy to find the slope and the 'y intercept' from the given equation.
| 1. | Meaning of y = mx + b |
| 2. | How to Find y = mx + b? |
| 3. | Writing an Equation in the Slope Intercept Form |
| 4. | Solved Examples on y mx b |
| 5. | Practice Questions on y mx b |
| 6. | FAQs on y mx b |
Meaning of y = mx + b
y = mx + b is the slope-intercept form of a staight line. In the equation y = mx + b for a straight line, m is called the slope of the line and b is the y-intercept of a line. y = mx+b, where
y ⇒ how far up or down is the line,
x ⇒ how far along is the line,
b ⇒ the value of y when x = 0 and
m ⇒ how steep the line is.
This is determined by m = (difference in y coordinates)/ (difference in x coordinates). Note that difference in y coordinates is indicated as rise or fall and difference in x coordinates is indicated as run.
How To Find y = mx + b?
y = mx + b is the formula used to find the equation of a straight line, when we know the slope(m) and the y-intercept (b) of the line. To determine m, we apply a formula based on the calculations. Let's derive this formula using the equation for the slope of a line. Let us consider a line whose slope is 'm' and whose y-intercept is 'b'. Let (x,y) be any other random point on the line whose coordinates are not known. We obtain the graph as follows.

We know that the equation for the slope of a line in the slope-intercept form is y = mx+b
Rewriting this, we get m = (y-b) / x
Thus the formula to find m = change in y/ change in x
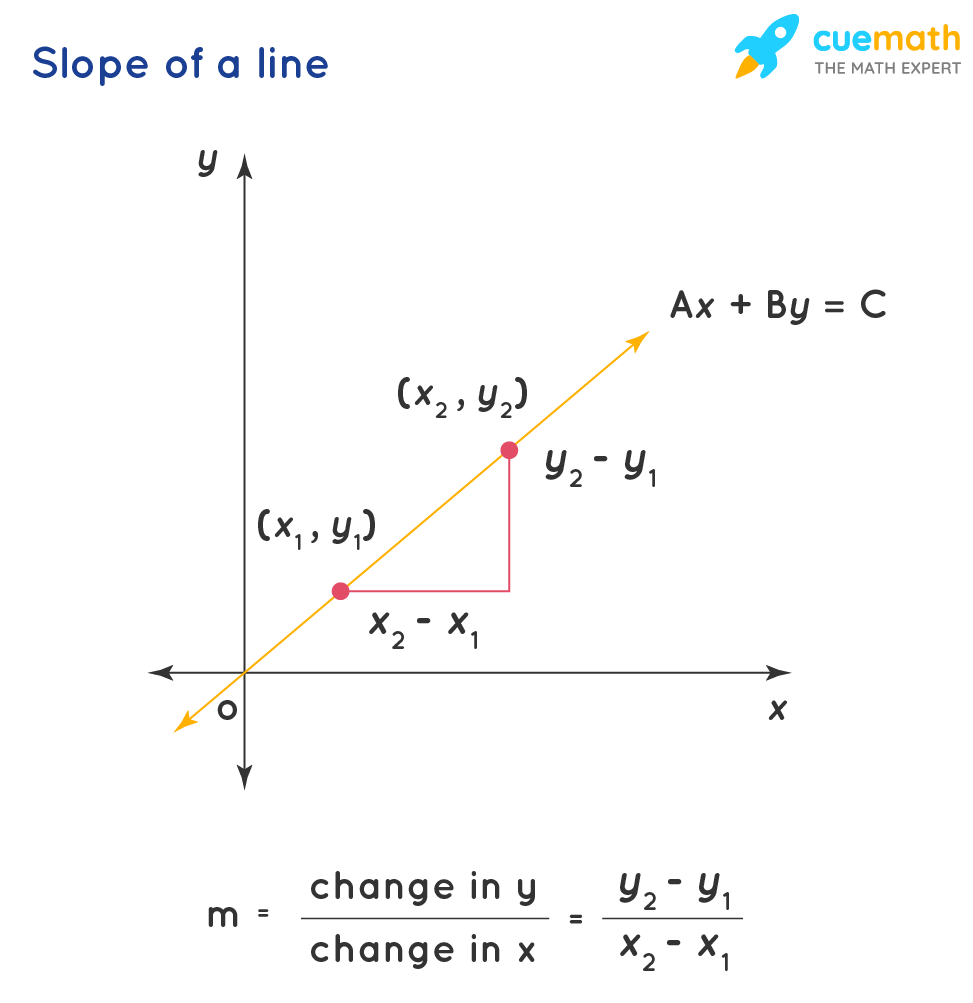
Let us derive the formula to find the value of the slope if two points \((x_{1},y_{1})\) and \((x_{2},y_{2})\) on the straight line are known. Then we have \(y_{1} = mx_{1} + b\) and \(y_{2} = mx_{2} + b\)
We know that, slope = change in y/ change in x
Substituting the values of y1 and y2, we get \[\begin{align}\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}&= \dfrac{(mx_{2}+b) - (mx_{1}+b)}{x_{2}-x_{1}}\\\\&=\dfrac{mx_{2}-mx_{1}}{x_{2}-x_{1}}\\\\&= \dfrac{m(x_{2}-x_{1})}{x_{2}-x_{1}}\\\\ &=m\end{align}\]
Thus we find that the slope (m) is calculated as (change in y)/ (change in x)
m = (difference in y coordinates)/ (difference in x coordinates)
To find the y-intercept or 'b', substitute the value of 'x' as 0 in the equation of a straight line, which is of the form Ax + By + C = 0. Consider an equation of a straight line : 3x + 5y = 10. To find the y-intercept, substitute the value of 'x' as 0 in the equation and solve for 'y'. On substituting 'x = 0' in the equation 3x + 5y =10, we get, 3(0) + 5y = 10
⇒5y = 10 and thus y = 10/5 ⇒ y = 2 or 'b' = 2.
Writing an Equation in The Slope Intercept Form
If the slope 'm' and y-intercept 'b' are given, then the equation of the straight line can be written in the form of 'y = mx +b'. For example, if the slope(m) for a line is 2 and the y-intercept 'b' is -1, then the equation of the straight line is written as y = 2x - 1. The slope value can be positive or negative. As we discussed in the earlier sections, in y = mx + b, 'm' represents the slope of the equation. To find the slope of a line, given its equation, we have to rearrange its terms to the slope-intercept form y = mx + b. Here, 'm' gives the slope and 'b' gives the y-intercept of the equation.
Let us consider the equation 2x + 3y = 6. We are required to find the slope and the y-intercept from the equation which is of the form Ax + By = C
We rewrite the standard form of the equation of the line to the slope-intercept form y = mx + b.
2x + 3y = 6
3y = 2x + 6
y = (-2/3) x + 2
Comparing the final equation with y = mx + b, we obtain the slope of the equation is m = -2/3 and the y-intercept of the equation is, b = 2 or (0,2).
Important Notes:
- The equation of the slope-intercept form of a line whose slope is 'm' and whose y-intercept is 'b' or (0,b) is y = mx + b.
- The equation of a horizontal line passing through (a,b) is of the form y = b.
- The equation of a vertical line passing through (a,b) is of the form x = a.
- m is calculated using the formula rise over run or (change in y)/ (change in x)
Topics Related to y = mx + b
Check out some interesting articles related to y = mx + b.
- Linear Equation Formula
- Equation of a Straight Line
- Linear Equations
- Linear Equations and Half Planes
- Point-slope formula
- Two Point Form
Solved Examples on y=mx+b
-
Example 1: Find the equation of the line whose graph contains the points (1,3) and (3,7)
Solution:
The required equation of the line is y = mx + b
Using the formula for slope, m = change in y / change in x = \(\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= (7-3)/ (3-1) = 4/2 ⇒ m = 2
To find the y-intercept b, we consider any one of the coordinates.
Let us use(1,3) and m = 2 and substitute the values in the equation \(y_{1} = mx_{1} + b\)
3 = 2(1) + b ⇒ b = 3 - 2 = 1
Applying, m =2 and b = 1 in the equation of the line(y = mx + b), we get y = 2x + 1 Thus the equation of the straight line is y = 2x + 1 -
Example 2: Find the slope-intercept form of a line with slope -2 and which passes through the point (-1.4).
Solution:
We know that the slope-intercept form of a line is y = mx + b.
It is given that slope (m) = -2 and the coordinates through which the line is passing through is (-1,4). Substituting the given values in the slope-intercept form equation we get, 4 = (-2) (-1) + b.
4 = 2 + b b = 4 - 2 = 2.
The slope intercept form of the line is y = - 2 x + 2.

FAQs on y mx b
What is y = mx + b?
y = mx + b is a representation of equation of a straight line. It is called as the slope intercept form. 'm' is referred to as the slope of the line, and 'b' refers to the 'y -intercept' of the line.
How to Find the Slope of a Line?
For two coordinates, (x1,y1) and (x2, y2), the slope of a line is the ratio of difference between the difference between the y coordinates and the difference between x coordinates, also known as the rise over the run. The formula to find the slope of a line is m = (y2-y1)/(x2-x1)
What is Slope-Intercept Form?
The equation of a straight line which is of the form y = mx + b, is called the slope intercept form. Here 'm' is the slope of the line and 'b' is the point at which the line intercepts the y - axis. An example for slope intercept form equation is y = 3x + 5
What is a Line With a Negative Slope?
A line for which the slope in negative is said to move from left to right in a graph. The slope of a line is found by the ration of difference in y-coordinates to the difference in x-coordinates. If this value is negative for a line, then the line has a negative slope.
What Does the Slope of a Line Mean?
The direction of a line is described by its slope. The slope can be positive or negative, based on its direction. A negative slope moves downward from left to right and a line with positive slope moves in the upward direction from right to left.
visual curriculum