The SSS Criterion - Proof

sss criterion

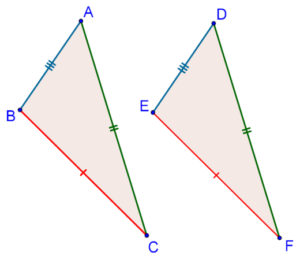
Let’s discuss the proof of the SSS criterion. Consider two triangles once again, ∆ABC and ∆DEF, with the same set of lengths, as shown below:

We have to show that ∆ABC ≡ ∆DEF. If we could show equality between even one pair of angles (say, ∠B = ∠E), then our proof would be complete, since the triangles would then be congruent by the SAS criterion.

Therefore, we begin our proof by supposing that none of the corresponding angles are equal. In particular, we suppose that: ∠B ≠ ∠E.

One of the two angles must then be less than the other. We suppose that ∠B < ∠E. Through B, draw BG such that ∠ABG = ∠DEF, and BG = EF, as shown below, and join A to G.

Now, observe that ∆ABG will be congruent to ∆DEF, by the SAS criteria. This leads to the following conclusions:

1. BG = EF, which is equal to BC. Thus, BG = BC.

2. AG = DF, which is equal to AC. Thus, AG = AC.

Now, take a good look at the following figure, in which we have highlighted to conclusions we just made (we have also marked X, the mid-point of GC):

Since BG = BC, ∆BGC is isosceles. Similarly, since AG = AC, ∆AGC is isosceles. What we have here is two isosceles triangles standing on the same base GC, where the perpendiculars from the vertex to the base (BX and AX) are in different directions. Is this possible? Can we have two isosceles triangles on the same base where the perpendiculars to the base are in different directions? No!

To put it even more simply, note that BX and AX should both be perpendicular to GC (why?). On the same segment, we cannot have two perpendiculars going in different directions. What does this mean?

This means that our original assumption of assuming that ∠B ≠ ∠E is flawed: ∠B must be equal to ∠E. Thus, the two triangles (∆ABC and ∆DEF) are congruent by the SAS criterion.