Perpendicular Bisector of a Chord

Theorem: The perpendicular bisector of any chord of a circle will pass through the center of the circle.

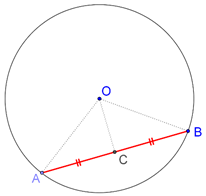
This is an extremely fundamental and widely used result on circles. Consider a chord AB of a circle with center O, as shown below. Let C be the mid-point of AB:

Proof: If we are able to prove that OC is perpendicular to AB, then we will be done, as then OC will be the perpendicular bisector of AB. Compare triangles OAC and OBC:

1. OA = OB (radii of the same circle)

2. OC = OC (common)

3. AC = BC (C is the mid-point of AB)

Thus, by the SSS criterion, \(\Delta OAC\) ≡\(\Delta OBC\) . This means that:

\(\angle ACO{\rm{ }} = \angle BCO{\rm{ }} = {\rm{ }}\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/\kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\rm{ }} \times {\rm{ }}{180^0} = {\rm{ }}{90^0}\)

This theorem leads us to a simple corollary, which is discussed next.