Linear Pair of Angles
In geometry, a linear pair of angles is a pair of adjacent angles formed when two lines intersect each other. Adjacent angles are formed when two angles have a common vertex and a common arm but do not overlap. The linear pair of angles are always supplementary as they form on a straight line. In other words, the sum of two angles in a linear pair is always 180 degrees.
| 1. | Definition of Linear Pair of Angles |
| 2. | Properties of Linear Pair of Angles |
| 3. | Linear Pair of Angles Vs Supplementary Angles |
| 4. | Linear Pair Postulate |
| 5. | FAQs |
Linear Pair of Angles Definition
When two lines intersect each other at a single point, linear pairs of angles are formed. If the angles so formed are adjacent to each other after the intersection of the two lines, the angles are said to be linear. If two angles form a linear pair, the angles are supplementary, whose measures add up to 180°. Hence, a linear pair of angles always add up to 180°.
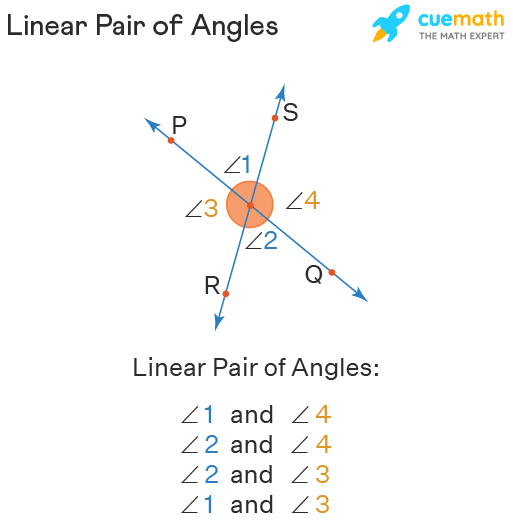
Properties of Linear Pair of Angles
There are some properties of linear pair of angles that make them unique and different from other types of angles. Look at the linear pair of angles properties listed below:
- The sum of two angles in a linear pair is always 180°.
- All linear pairs of angles are adjacent angles but all adjacent angles are not linear pairs.
- Linear pair of angles share a common vertex and a common arm between them.
- They always form on a straight line.
- They can be considered as two parts of a 180-degree angle or a straight angle.
Linear Pair of Angles Vs Supplementary Angles
In geometry, there are two types of angles whose sum is 180 degrees. They are linear pairs of angles and supplementary angles. We often say that the linear pair of angles are supplementary, but do you know that these two types of angles are not the same? Let us understand the difference between supplementary angles and linear pair of angles through the table given below:
| Linear Pair of Angles | Supplementary Angles |
|---|---|
| These angles are always adjacent to each other. It means, a pair of angles whose sum is 180 degrees and they lie next to each other sharing a common vertex and a common arm are known as linear pair of angles. | These angles need not be adjacent. Their sum is also 180°. |
| All linear pairs are supplementary angles too. | All supplementary angles are not linear pairs. |
| Example: ∠1 and ∠2 in the image given below. | Example: ∠A and ∠B, ∠1 and ∠2 (in the image below). |
In the image below, it can be clearly seen that both the pairs of angles are supplementary, but ∠A and ∠B are not linear pairs because they are not adjacent angles.
Linear Pair Postulate
The linear pair postulate states that if a ray stands on a line, then the sum of two adjacent angles is 180º. Will the converse of this statement be true? That is if the sum of a pair of adjacent angles is 180º, will the non-common arms of the two angles form a line? Yes, the converse is also true. These two axioms are grouped together as the linear pair axiom. In the figure below, ray QS stands on a line PR forming a linear pair of angles ∠1 and ∠2.
Important Notes
- In a linear pair, if the two angles have a common vertex and a common arm, then the non-common side makes a straight line and the sum of the measure of angles is 180°.
- Linear pairs are always supplementary.
- Linear pairs of angles are not always congruent.
► Related Topics
Check these interesting articles related to the linear pair of angles in geometry.
Linear Pair of Angles Examples
-
Example 2: In the given figure, if POQ is a straight line and ∠POC = ∠COQ, then show that ∠POC = 90°.
Solution:Since ray OC stands on line PQ. So, by linear pair axiom, ∠POC + ∠COQ = 180°. But ∠POC = ∠COQ (given).
⇒ ∠POC + ∠POC = 180°
⇒ 2∠POC = 180°⇒ ∠POC = 180°/2 = 90°
⇒ ∠POC = 90°
Hence Proved.
FAQs on Linear Pair of Angles
What is a Linear Pair of Angles?
In math, a linear pair of angles are those two adjacent angles whose sum is 180°. They are drawn on a straight line with a ray that acts as a common arm between the angles.
How Do you Find the Linear Pair of an Angle?
If there is a pair of adjacent angles, then this pair is a linear pair if the sum of the (measures of the) two angles will be 180°. So, linear pair of angles always add up to 180°. For example, the linear pair of 30° is 150°, the linear pair of 70° is 110°, etc.
Is a Linear Pair always Supplementary?
Supplementary is one of the necessary conditions for being a linear pair. Hence, linear pairs will always be supplementary. As per their definition, a linear pair forms a straight angle that measures 180º.
How Many Angles are there in a Linear Pair?
In a linear pair, two adjacent angles are formed by two intersecting lines. A straight angle has an angle of 180°, so a linear pair of angles must add up to 180°.
Are Linear Pair of Angles always Congruent?
Linear pairs of angles are not always congruent. Only when the measure of each of the angles is 90°, a linear pair of angles is said to be congruent.
Can 3 Angles Form a Linear Pair?
A linear pair can be defined as two adjacent angles that add up to 180° or two angles which when combined together form a line or a straight angle. Three angles can be supplementary, but not necessarily adjacent. For instance, angles in any triangle add up to 180° but they don't form a linear pair.