Intercept Form

The intercept form of the equation of a line is x/a + y/b = 1. This is one of the important forms of equations of a line. Also, the sign of the intercepts in this equation helps us to know the location of the line with respect to the coordinate axes. The intercept form of the equation of the line can be understood as the line which makes a right triangle with the coordinates axes, with the sides of lengths as 'a' units and 'b' units respectively.

Let us now check the equation of intercept form, the graph of intercept form, and the derivation of intercept form, from other forms of equations of a line.

The intercept form of the equation of a line has an equation x/a + y/b = 1, where 'a' is the x-intercept, and 'b' is the y-intercept. The x-intercept is the shortest distance of the point on the x-axis from the origin, where the line cuts the x-axis, and the y-intercept is the shortest distance of the point on the y-axis from the origin, where the line cuts the y-axis. Also considering the points, the line cuts the x-axis at the point(a, 0), and it cuts the y-axis at the point(0, b).

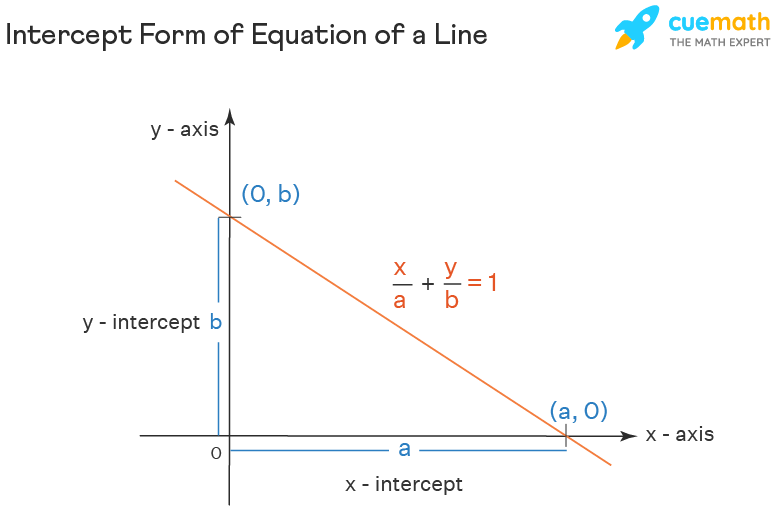
Intercept Form of Equation of a Line: x/a + y/b = 1.

Here x, y, are the variables in the equation, a, b, are the x-intercept, and the y-intercept in the equation. This equation has a slope of -b/a.

Since this line cuts both the coordinate axes, it makes a right triangle with the coordinate axes, and the area of the right angled triangle is equal to the product of half of its intercepts 1/2 · |ab|. Further, the intercept form of the equation of a line can be simplified and represented as the standard form of the equation of a line as bx + ay = ab.

The graph of intercept form cuts the coordinate axes at the two points on the x-axis and the y-axis respectively. The two points are at distances of 'a' units and 'b' units from the origin, and on the x and y-axis respectively. Since the line cuts an intercept of 'a' units on the x-axis, it passes through the point (a, 0) on the x-axis. and it cuts an intercept of 'b' units on the y-axis, it passes through the point (0, b) on the y-axis respectively.

The intercept form of the equation of the line can be derived from the other forms of equations of a line. Here we derive the intercept form of the equation of the line from the two-point form of equation of a line.

Two Point Form

The two point form of equation of a line requires two points on the line. The equation of a line passing through the two-points (a, 0), and (0, b) can be found using the two-point form of the equation of a line. The equation of the line passing through the two points (a, 0), and (0, b) respectively is as follows.

y - 0 = (b - 0)/(0 - a).(x - a)
y = b/-a.(x - a)
-ay = b(x - a)
-ay = bx - ab
ab = bx + ay
bx + ay = ab
(bx + ay)/ab = 1
bx/ab + ay/ab = 1
x/a + y/b = 1

Important Notes on Intercept Form:

The following points help in clearly understanding the details of the intercept form of the equation of a line.

• The intercept form of the equation of a line is x/a + y/b = 1.
• The intercept form of the equation of a line makes the x-intercept of 'a' units, and the y-intercept of 'b' units.
• Based on the sign of the intercepts we can find the quadrants through which the line passes through.
• The intercept form of the equation of a line makes a right triangle with the coordinate axes, and the area of this right triangle is 1/2 · |ab|.

☛ Related Topics:

The following related topics are helpful for a better understanding of the intercept form of the equation of a line.

• Coordinate Geometry
• Coordinate Plane
• Cartesian Coordinates
• y = mx + b

What is Intercept Form of Equation of a Line?

The Intercept Form of Equation of a Line is of the Form x/a + y/b = 1. Here 'a' is the x-intercept, and 'b' is the y-intercept. The value of 'a' is the distance from the origin, and on the x-axis, at which this line cuts the x-axis, and the value of 'b' is the distance from the origin, and on the y-axis, at which this line cuts the y-axis. The signs of these intercepts helps us to know the quadrants through which this line is passing.

What Can be Derived From the Intercept Form of Equation of A Line?

The intercept form of the equation of the straight line helps us to derive two important aspects. Firstly, the intercept form of equation of line ( x/a + y/b = 1), helps us in knowing the x-intercept and the y-intercept of the line. Secondly, based on the signs of the intercepts, we can find the quadrant through which this line passes.

How To Convert Intercept Form to Standard Form of Equation of a Line?

The intercept form of the equation of the line can be easily transformed into the standard form of the equation of a line. The intercept form of the equation of the line is x/a + y/b = 1, and the standard form of the equation of the line is ax + by + c = 0. The steps of transformation from intercept form to standard form is as follows.

x/a + y/b = 1
(bx + ay)/ab = 1
bx + ay = ab

This above-derived equation of a line is of the form ax + by + c = 0, and it represents the standard equation of a line.

What Are the Other Forms of Equations of a Line, Similar to Intercept Form?

The other forms of equations of a line, similar to intercept form, are as follows.

• Point Slope Form: y - y₁ = m(x - x₁).
• Two Point Form: y - y₁ = (y₂ - y₁)/(x₂ - x₁) · (x - x₁)
• Slope Intercept Form: y = mx + c
• Intercept Form: x/a + y/b = 1
• Normal Form: x cos θ + y sin θ = P