Inscribed Angle Theorem
The inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle. In this section, we will learn about the inscribed angle theorem, the proof of the theorem, and solve a few examples.
| 1. | What is Inscribed Angle Theorem? |
| 2. | Properties of Inscribed Angle Theorem |
| 3. | Proof of Inscribed Angle Theorem |
| 4. | FAQs on Inscribed Angle Theorem |
What is Inscribed Angle Theorem?
The inscribed angle theorem is also called the angle at the center theorem as the inscribed angle is half of the central angle. Since the endpoints are fixed, the central angle is always the same no matter where it is on the same arc between the endpoints. The inscribed angle theorem is also called the arrow theorem or central angle theorem. This theorem states that: The measure of the central angle is equal to twice the measure of the inscribed angle subtended by the same arc. OR. An inscribed angle is half of a central angle that subtends the same arc. OR. The angle at the center of a circle is twice any angle at the circumference subtended by the same arc. We need to keep in mind these three terms for the theorem:
- An inscribed angle is an angle whose vertex lies on the circle with its two sides as the chords of the same circle.
- A central angle is an angle whose vertex lies at the center of the circle with two radii as the sides of the angle.
- The intercepted arc is an angle formed by the ends of two chords on a circle's circumference.

In the above image, AB = the intercepted arc, θ = the inscribed angle, and 2θ = the central angle.
Properties of Inscribed Angle Theorem
An inscribed angle theorem has three basic properties that are connected with the central angle, they are:
- The inscribed angle subtended by the same arc is equal. (see below image for reference)
- The inscribed angle in a semicircle is 90°.
- Central angles subtended by arcs are of the same length.
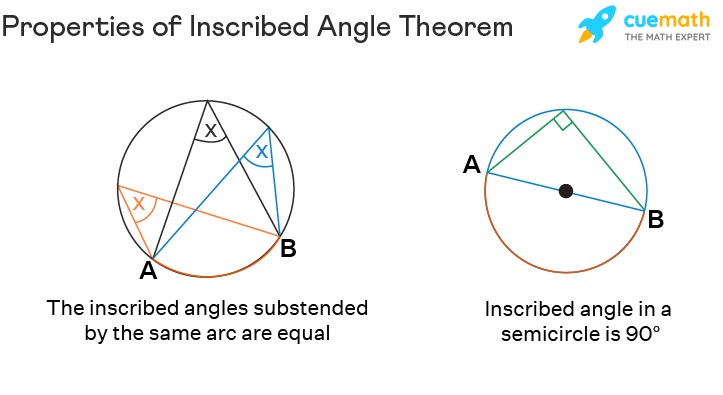
In the image above, we see that....
Proof of Inscribed Angle Theorem
To prove the inscribed angle theorem we need to consider three cases:
- Inscribed angle is between a chord and the diameter of a circle.
- Diameter is between the rays of the inscribed angle.
- Diameter is outside the rays of the inscribed angle.
Case 1. Inscribed angle is between a chord and the diameter of a circle.
Here we need to prove that ∠AOB = 2θ

In the above image, let us consider that ∆OBD is an isosceles triangle where OD = OB = radius of the circle. Therefore, ∠ODB = ∠DBO = inscribed angle = θ. The diameter AD is a straight line hence ∠BOD = 180 - ∠AOB(call it x). According to the angle sum property, ∠ODB + ∠DBO + ∠BOD = 180°.
θ + θ + (180 - x) = 180
2θ + 180 - x = 180
2θ - x = 180 - 180
2θ - x = 0
x = 2θ.
Therefore, ∠AOB = 2θ. Hence proved.
Case 2: Diameter is between the rays of the inscribed angle.
Here we need to prove that ∠ACB = 2θ

In the above image, we draw a diameter in dotted lines that bisect both the angles as seen i.e. θ = θ1 + θ2 and a = a1 + a2. From case 1, we already that a1 = 2θ1 and a2 = 2θ2. When we add the angles, we get:
a1 + a2 = 2θ1 + 2θ2
a1 + a2 = 2 (θ1 + θ2)
a1 + a2 = 2θ
a = 2θ
Hence proved that ∠ACB = 2θ.
Case 3: Diameter is outside the rays of the inscribed angle.
Need to prove a = 2θ in the below circle.

From the above circle, we already know,
a1 = 2θ1
2 (θ1 + θ) = a1 + a
But, a1 = 2θ1 and a2 = 2θ2. By substituting we get,
2θ1 + 2θ = 2θ1 + a
a = 2θ.
Hence proved.
Related Topics
Listed below are a few topics related to the inscribed angle theorem, take a look.
Examples on Inscribed Angle Theorem
-
Example 1: Jim uses a compass to draw an arc of length 11 inches and a radius of 7 inches. Without using a protractor, how can Jim calculate the angle of this arc?
Solution:Length of the arc = 11 inches
Radius of the arc = 7 inches
Angle of the arc = (length of arc × 360°)/(2 π r)
Angle = (11 × 360°)/ (2 × 22/7 × 7)
Angle = 90°
Therefore, the angle of the arc is 90°.
-
Example 2: Find the missing angle x in the diagram below.

Solution:
We need to find the value of x. One angle is given as 80°.
By inscribed angle theorem we know that the central angle = 2 × inscribed angle
x = 2 × 80
x = 160
Therefore, the value of x = 160°.

FAQs on Inscribed Angle Theorem
What is Meant by Inscribed Angle Theorem?
Inscribed angle theorem is also called as central angle theorem where it states that the angle subtended by an arc at the center of the circle is double the angle subtended by it at any other point on the circumference of the circle.
What Does the Inscribed Angle Theorem State?
The inscribed angle theorem states that an angle inscribed in a circle is half of the central angle that is subtends the same arc on the circle.
What is an Inscribed Angle?
The angle subtended by an arc at any point on the circle is called an inscribed angle.
What is the Difference Between Central Angle and Inscribed Angle?
Central angle is the angle subtended by an arc at the center of a circle. Inscribed angle is an angle subtended by an arc at any point on the circumference of a circle.
visual curriculum
