Hyperbola

In mathematics, a hyperbola is an important conic section formed by the intersection of the double cone by a plane surface, but not necessarily at the center. A hyperbola is symmetric along the conjugate axis, and shares many similarities with the ellipse. Concepts like foci, directrix, latus rectum, eccentricity, apply to a hyperbola. A few common examples of hyperbola include the path followed by the tip of the shadow of a sundial, the scattering trajectory of sub-atomic particles, etc.

Here we shall aim at understanding the definition, formula of a hyperbola, derivation of the formula, and standard forms of hyperbola using the solved examples.

A hyperbola, a type of smooth curve lying in a plane, has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. A hyperbola is a set of points whose difference of distances from two foci is a constant value. This difference is taken from the distance from the farther focus and then the distance from the nearer focus. For a point P(x, y) on the hyperbola and for two foci F, F', the locus of the hyperbola is PF - PF' = 2a.

Hyperbola Definition

A hyperbola, in analytic geometry, is a conic section that is formed when a plane intersects a double right circular cone at an angle such that both halves of the cone are intersected. This intersection of the plane and cone produces two separate unbounded curves that are mirror images of each other called a hyperbola.

Let us check through a few important terms relating to the different parameters of a hyperbola.

Foci of hyperbola: The hyperbola has two foci and their coordinates are F(c, o), and F'(-c, 0).

Center of Hyperbola: The midpoint of the line joining the two foci is called the center of the hyperbola.

Major Axis: The length of the major axis of the hyperbola is 2a units.

Minor Axis: The length of the minor axis of the hyperbola is 2b units.

Vertices: The points where the hyperbola intersects the axis are called the vertices. The vertices of the hyperbola are (a, 0), (-a, 0).

Latus Rectum of Hyperbola: The latus rectum is a line drawn perpendicular to the transverse axis of the hyperbola and is passing through the foci of the hyperbola. The length of the latus rectum of the hyperbola is 2b²/a.

Transverse Axis: The line passing through the two foci and the center of the hyperbola is called the transverse axis of the hyperbola.

Conjugate Axis: The line passing through the center of the hyperbola and perpendicular to the transverse axis is called the conjugate axis of the hyperbola.

Eccentricity of Hyperbola: (e > 1) The eccentricity is the ratio of the distance of the focus from the center of the hyperbola, and the distance of the vertex from the center of the hyperbola. The distance of the focus is 'c' units, and the distance of the vertex is 'a' units, and hence the eccentricity is e = c/a.

Hyperbola Equation

The below equation represents the general equation of a hyperbola. Here the x-axis is the transverse axis of the hyperbola, and the y-axis is the conjugate axis of the hyperbola.

\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\)

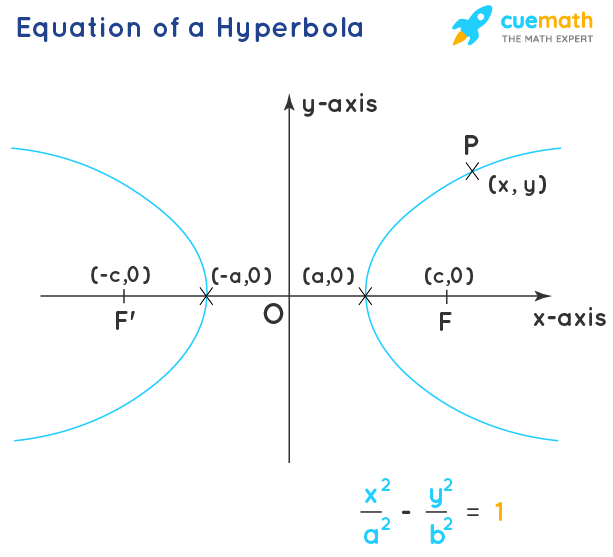
Let us understand the standard form of the hyperbola equation and its derivation in detail in the following sections.

There are two standard equations of the Hyperbola. These equations are based on the transverse axis and the conjugate axis of each of the hyperbola. The standard equation of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) has the transverse axis as the x-axis and the conjugate axis is the y-axis. Further, another standard equation of the hyperbola is \(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\) and it has the transverse axis as the y-axis and its conjugate axis is the x-axis. The below image shows the two standard forms of equations of the hyperbola.

As per the definition of the hyperbola, let us consider a point P on the hyperbola, and the difference of its distance from the two foci F, F' is 2a.

PF' - PF = 2a

Let the coordinates of P be (x, y) and the foci be F(c, o) and F'(-c, 0)

\(\sqrt{(x + c)^2 + y^2}\) - \(\sqrt{(x - c)^2 + y^2}\) = 2a

\(\sqrt{(x + c)^2 + y^2}\) = 2a + \(\sqrt{(x - c)^2 + y^2}\)

Now we need to square on both sides to solve further.

(x + c)² + y² = 4a² + (x - c)² + y² + 4a\(\sqrt{(x - c)^2 + y^2}\)

x² + c² + 2cx + y² = 4a² + x² + c² - 2cx + y² + 4a\(\sqrt{(x - c)^2 + y^2}\)

4cx - 4a² = 4a\(\sqrt{(x - c)^2 + y^2}\)

cx - a² = a\(\sqrt{(x - c)^2 + y^2}\)

Squaring on both sides and simplifying, we have.

\(\dfrac{x^2}{a^2} - \dfrac{y^2}{c^2 - a^2} =1\)

Also, we have c² = a² + b², we can substitute this in the above equation.

\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} =1\)

Therefore, the standard equation of the Hyperbola is derived.

Hyperbola is an open curve that has two branches that look like mirror images of each other. For any point on any of the branches, the absolute difference between the point from foci is constant and equals to 2a, where a is the distance of the branch from the center. The Hyperbola formula helps us to find various parameters and related parts of the hyperbola such as the equation of hyperbola, the major and minor axis, eccentricity, asymptotes, vertex, foci, and semi-latus rectum.

Equation of hyperbola formula: (x - \(x_0\))² / a² - ( y - \(y_0\))² / b² = 1

Major and minor axis formula: y = y\(_0\) is the major axis, and its length is 2a, whereas x = x\(_0\) is the minor axis, and its length is 2b

Eccentricity(e) of hyperbola formula: e = \(\sqrt {1 + \dfrac {b^2}{a^2}}\)

Asymptotes of hyperbola formula:
y = y\(_0\) − (b / a)x + (b / a)x\(_0\)
y = y\(_0\) + (b / a)x - (b / a)x\(_0\)

Vertex of hyperbola formula:
(a, y\(_0\)) and (−a, y\(_0\))

Focus(foci) of hyperbola:
(x\(_0\) + \(\sqrt{a^2+b^2} \),y\(_0\)), and (x\(_0\) _- \(\sqrt{a^2+b^2} \),y\(_0\))

Semi-latus rectum(p) of hyperbola formula:
p = b² / a

where,

• x\(_0\), y\(_0\) are the center points.
• a = semi-major axis.
• b = semi-minor axis.

Example: The equation of the hyperbola is given as (x - 5)²/4² - (y - 2)²/ 2² = 1. Use the hyperbola formulas to find the length of the Major Axis and Minor Axis.

Solution:

Using the hyperbola formula for the length of the major and minor axis

Length of major axis = 2a, and length of minor axis = 2b

Length of major axis = 2 × 4 = 8, and Length of minor axis = 2 × 2 = 4

Answer: The length of the major axis is 8 units, and the length of the minor axis is 4 units.

All hyperbolas share common features, consisting of two curves, each with a vertex and a focus. The transverse axis of a hyperbola is the axis that crosses through both vertices and foci, and the conjugate axis of the hyperbola is perpendicular to it. We can observe the graphs of standard forms of hyperbola equation in the figure below. If the equation of the given hyperbola is not in standard form, then we need to complete the square to get it into standard form.

We can observe the different parts of a hyperbola in the hyperbola graphs for standard equations given below.

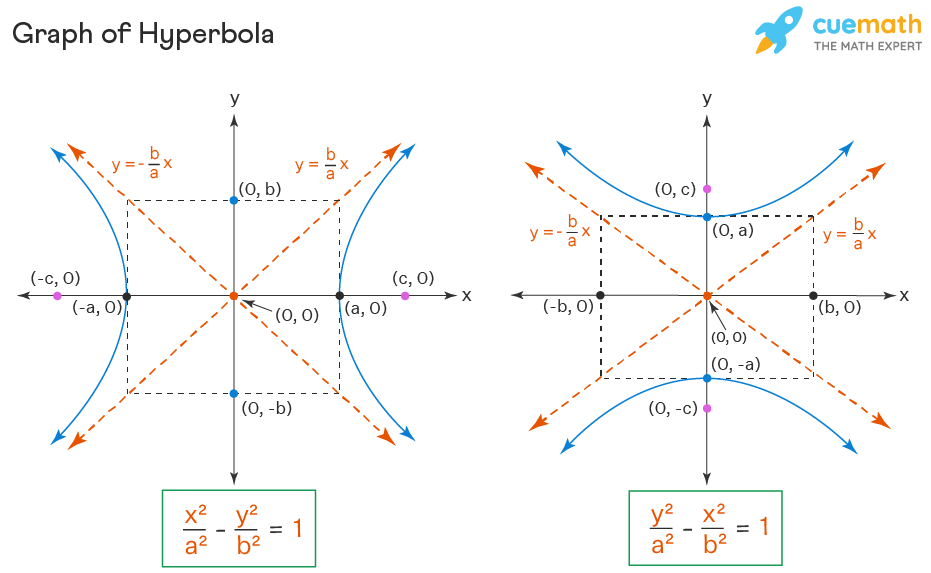
Here,

• If the foci lie on the x-axis, the standard form of a hyperbola can be given as,
  \(\dfrac{(x-h)^2}{a^2} - \dfrac{(y-k)^2}{b^2} = 1\)
• If the foci lie on the y-axis, the standard form of the hyperbola is given as,
  \(\dfrac{(y-k)^2}{a^2} - \dfrac{(x-h)^2}{b^2} = 1\)
• Coordinates of the center: (h, k).
• Coordinates of vertices: (h+a, k) and (h - a,k)
• Co-vertices correspond to b, the ” minor semi-axis length”, and coordinates of co-vertices: (h,k+b) and (h,k-b).
• Foci have coordinates (h+c,k) and (h-c,k). The value of c is given as, c² = a² + b².
• Slopes of asymptotes: y = ±(b/a)x.

The following important properties related to different concepts help in understanding hyperbola better.

Asymptotes: The pair of straight lines drawn parallel to the hyperbola and assumed to touch the hyperbola at infinity. The equations of the asymptotes of the hyperbola are y = bx/a, and y = -bx/a respectively.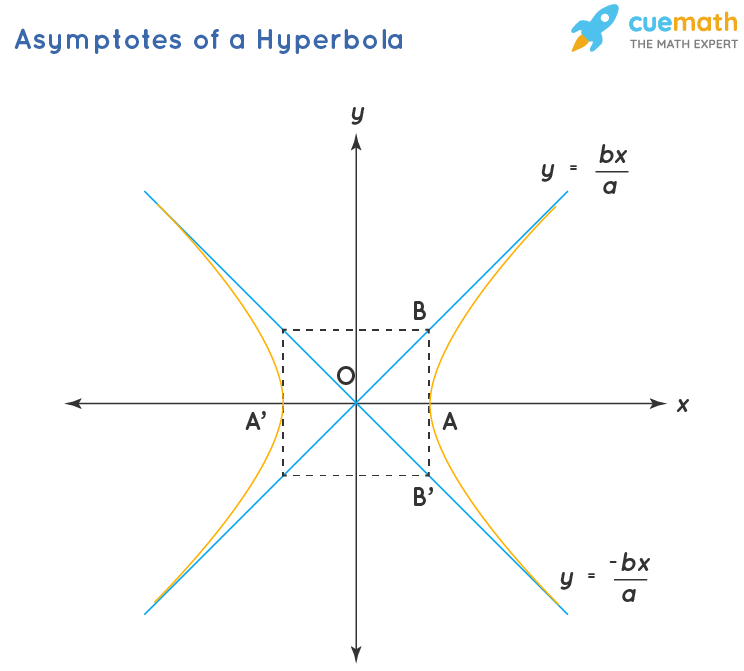

Rectangular Hyperbola: The hyperbola having the transverse axis and the conjugate axis of the same length is called the rectangular hyperbola. Here, we have 2a = 2b, or a = b. Hence the equation of the rectangular hyperbola is equal to x² - y² = a²

Parametric Coordinates: The points on the hyperbola can be represented with the parametric coordinates (x, y) = (asecθ, btanθ). These parametric coordinates representing the points on the hyperbola satisfy the equation of the hyperbola.

Auxilary Circle: A circle drawn with the endpoints of the transverse axis of the hyperbola as its diameter is called the auxiliary circle. The equation of the auxiliary circle of the hyperbola is x² + y² = a².

Direction Circle: The locus of the point of intersection of perpendicular tangents to the hyperbola is called the director circle. The equation of the director circle of the hyperbola is x² + y² = a² - b².

Related Articles on Hyperbola:

The following topics are helpful for a better understanding of the hyperbola and its related concepts.

• Coordinate Geometry
• Conics in Real Life
• Cartesian Coordinates
• Parabola

What is Hyperbola in Conic Section?

A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. The two fixed points are called the foci of the hyperbola, and the equation of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\). Here a is called the semi-major axis and b is called the semi-minor axis of the hyperbola.

What is the Equation of Hyperbola?

The equation of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\). Here 'a' is the sem-major axis, and 'b' is the semi-minor axis. There are two standard forms of equations of a hyperbola.

How to Find the General Equation of a Hyperbola?

The equation of the hyperbola can be derived from the basic definition of a hyperbola: A hyperbola is the locus of a point whose difference of the distances from two fixed points is a constant value. Let the fixed point be P(x, y), the foci are F and F'. Then the condition is PF - PF' = 2a. The difference is taken from the farther focus, and then the nearer focus. This on further substitutions and simplification we have the equation of the hyperbola as \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\).

What is a Rectangular Hyperbola?

The hyperbola having the major axis and the minor axis of equal length is called a rectangular hyperbola. Hence we have 2a = 2b, or a = b. The equation of the rectangular hyperbola is x² - y² = a².

What is the Standard Equation of Hyperbola?

There are two standard equations of the Hyperbola. These equations are given as,

• \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\), for an hyperbola having the transverse axis as the x-axis and the conjugate axis is the y-axis.
• \(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\), for an hyperbola having the transverse axis as the y-axis and its conjugate axis is the x-axis.

What is the Eccentricity of Hyperbola?

The eccentricity of the hyperbola is greater than 1. (e > 1). The eccentricity is the ratio of the distance of the focus from the center of the ellipse, and the distance of the vertex from the center of the ellipse. The distance of the focus is 'c' units, and the distance of the vertex is 'a' units, and hence the eccentricity is e = c/a. Also here we have c² = a² + b².

What is the Foci of a Hyperbola?

The hyperbola has two foci on either side of its center, and on its transverse axis. The hyperbola \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) has two foci (c, 0), and (-c, 0).

What is the Conjugate Axis of a Hyperbola?

The axis line passing through the center of the hyperbola and perpendicular to its transverse axis is called the conjugate axis of the hyperbola. The conjugate axis of the hyperbola having the equation \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) is the y-axis.

What are Asymptotes of Hyperbola?

The asymptotes are the lines that are parallel to the hyperbola and are assumed to meet the hyperbola at infinity. The equation of asymptotes of the hyperbola are y = bx/a, and y = -bx/a. The equation of pair of asymptotes of the hyperbola is \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 0\).

What are the Vertices of a Hyperbola?

The vertices of a hyperbola are the points where the hyperbola cuts its transverse axis. The hyperbola has only two vertices, and the vertices of the hyperbola \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) is (a, 0), and (-a, 0) respectively.

How to Find Transverse Axis of a Hyperbola?

The transverse axis of a hyperbola is a line passing through the center and the two foci of the hyperbola. A hyperbola with an equation \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) had the x-axis as its transverse axis.