Apothem
Tim and Sam were finding the area of various regular polygons. Tim divided the polygons into triangles and was trying to calculate the area of the polygons, which took him too long. On the other hand, Sam found the area of the polygons easily, as he knew the length of the apothem. So let's learn about apothem today!
Before we get started, check out this interesting simulation to identify the apothem for various polygons. This apothem calculator will help you understand the lesson better.
Lesson Plan
What Is Meant by Apothem?
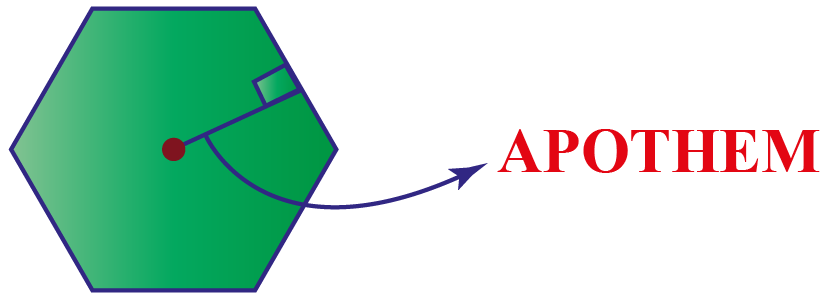
Apothem is a line drawn from the center of any polygon to the midpoint of one of the sides.
Formulas Used to Calculate the Apothem Length
The apothem formula, when the side length is given is:
| \(a\) = \(\begin{align}\frac{S}{2\,\, \text{tan}\left ( \frac{180}{n} \right )}\end{align}\) |
Where,
\(a\) = apothem length
\(s\) = side length
\(n\) = number of sides of a polygon.
The apothem formula , when the radius is given is:
| \(a\) = \(r.cos\frac{180}{n}\) |
\(r\) = radius.
\(n\) = number of sides
\(Cos\) = cosine function which is calculated in degrees.
We can use the apothem area formula of a polygon to calculate the length of the apothem.
| \(A\) = \(\dfrac{1}{2}aP\) |
Where,
\(A\) = area of the polygon
\(a\) = apothem.
\(P\) = perimeter
How to Calculate Area of a Polygon Using Apothem?
To calculate the area of a polygon with the help of apothem, we use the formula:
\(A\) = \(\dfrac{1}{2}aP\)
Where,
\(a\) = apothem.
\(P\) = perimeter.
Example: Find the area of a regular hexagon, if the side length is \(5\) inches, and the apothem is \(3\) inches.
\(A\) = \(\dfrac{1}{2}aP\)
As we know perimeter:
\[\begin{align}P &= [\text{side length}]\times [\text{no. of sides}]\\&= 5\times6 = 30\end{align}\]
After the perimeter is calculated, we use it in the formula of Area = \(A\) = \(\dfrac{1}{2}aP\)
\[\begin{align}A &= \dfrac{1}{2}aP \\
& = \dfrac{1}{2} \left ( 3\right )\left (30 \right )\\& = 45 \text{ inches}^2\end{align}\]

- The apothem is always perpendicular to the side on which it ends.
- A regular polygon has all its sides and angles equal.
Solved Examples
| Example 1 |
Help Bryan find the length of the apothem of a regular pentagon of side = \(10\) inches and area \(150\sqrt{3}\,\,\text {inches}^{2}\).

Solution
Given,
\(L\) = \(10\) inches.
\(A\) = \(150\sqrt{3}\,\,\text {inches}^{2}\)
So, the perimeter will be \(P\) = \(10\times 5\) = \(50\) inches.
\[\begin{align}A&=\dfrac{1}{2}aP\\
150\sqrt{3}&= \dfrac{1}{2}a\times 50\\
25a&=150\sqrt{3}\\
a&=\dfrac{150\sqrt{3}}{25}\\
a&=6\sqrt{3}\text{ inches}\end{align}\]
Therefore, Apothem = \(6\sqrt{3}\) inches.
| \(\therefore\) \(a\) = \(6\sqrt{3}\) inches |
| Example 2 |
Can you help Dylan calculate the area of a regular hexagon of side 8 inches and apothem \(4\sqrt{3}\), using the area of polygon formula?

Solution
Given,
side length = 8 inches.
perimeter \(P\) = \(L\times n\)
= \(8\times 6\)
= \(48\) inches
Area of polygon = \[\begin{align}A& = \dfrac{1}{2}aP\\&= \dfrac{1}{2}\times4\sqrt{3}\times 48\\&= 96\sqrt{3} \text{ inches}^2\end{align}\]
| \(\therefore\) The area of the polygon is \(96\sqrt{3} \text{ inches}^2\) |
| Example 3 |
Emily's teacher asked her to calculate the area of a regular hexagon, whose apothem is 7 inches and perimeter 48 inches.
Solution
Given,
\(a\) = 7 inches.
\(P\) = 48 inches.
Thus, the Area of hexagon will be:\[\begin{align}&\frac{1}{2}aP\\
&=\frac{1}{2}\times 7\times 48\\
&=\frac{1}{2}\times 336\\
&=\frac{336}{2}\\
&=168 \text{ inches}^2\end{align}\]
| \(\therefore\) \(A\) = \(168 \text{ inches}^2\) |
| Example 4 |
Can you help Jose calculate the length of the apothem of a square, which has a side length of 3 inches?
Solution
The formula for calculating apothem, when side length is given is:
\(a\) = \(\begin{align}\frac{S}{2 \,\,\text{tan}\left ( \frac{180}{n} \right )}\end{align}\)
\[\begin {align}a &=\dfrac{S}{2\,\,\text{tan}\left ( \dfrac{180}{n} \right)}\\
&=\dfrac{3}{2\,\,\text{tan}\left ( \dfrac{180}{4} \right)}\\
&=\dfrac{3}{2\,\,\text{tan} 45}\\
&=\dfrac{3}{2\times 1}\\
&=\dfrac{3}{2}\\
&=1.5\text{ inches}\end{align}\]
| \(\therefore\) The length of apothem is \(1.5\text{ inches}\) |

- Devin wanted to calculate the area of a regular octagon of side 12 inches and apothem 14.5 inches. Help him find the answer.
Interactive Questions
Here are a few activities for you to practice.
Select/Type your answer and click the "Check Answer" button to see the result.
Let's Summarize
We hope you enjoyed learning about apothem with the simulations and practice questions. Now you will be able to easily solve problems related to the apothem.
About Cuemath
At Cuemath, our team of math experts is dedicated to making learning fun for our favorite readers, the students!
Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.
Be it worksheets, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we at Cuemath believe in.
Frequently Asked Questions (FAQs)
1. Is the apothem the same as the radius?
Apothem is also a radius, but when we talk about radius, we usually refer to a circle or a sphere.
However, when we talk about apothem, it can be any other polygon as well, such as the square, triangle, or hexagon.
2. Is the Apothem Equal to the Side Length?
No, an apothem's length is not always equal to its side length. However, if we know the side length of a polygon, the apothem can be calculated.
3. What is the Apothem of a Square?
The apothem of a square is equal to half of its side length.