Angles of Quadrilateral
The interior angles of a quadrilateral always sum up to 360°. Quadrilaterals are four-sided polygons with four vertices and four interior angles. There are different types of quadrilaterals such as the square, rectangle, rhombus, and so on. The unknown angles of a quadrilateral can be easily calculated if the other angles are known because the interior angles of a quadrilateral always sum up to 360°. Let us learn more about the angles of quadrilateral in this article.
| 1. | Angles of Quadrilateral |
| 2. | Interior and Exterior Angles of Quadrilateral |
| 3. | Angles of Quadrilateral Formula |
| 4. | Angles of Quadrilateral Inscribed in a Circle |
| 5. | FAQs on Angles of Quadrilateral |
Angles of Quadrilateral
There are four interior angles in a quadrilateral and they add up to a sum of 360°. This value is obtained using the angle sum property of a quadrilateral. According to the angle sum property of a polygon, the sum of the interior angles of a polygon can be calculated with the help of the number of triangles that can be formed in it. These triangles are formed by drawing diagonals from a single vertex. To make things easier, this can be calculated by a formula, which says that if a polygon has 'n' sides, there will be (n - 2) triangles inside it.
The sum of the interior angles of a polygon can be calculated with the formula: S = (n − 2) × 180°, where 'n' represents the number of sides of the given polygon. For example, let us take a quadrilateral and apply the formula using n = 4, we get: S = (n − 2) × 180°, S = (4 − 2) × 180° = 2 × 180° = 360°. Therefore, according to the angle sum property of a quadrilateral, the sum of its interior angles is always 360°. This property helps in finding the unknown angles of quadrilateral. If the other angles are known, then their sum can be subtracted from 360° to get the value of the unknown angle.
Interior and Exterior Angles of Quadrilateral
There are 4 interior angles and 4 exterior angles in a quadrilateral. Observe the following figure to understand the difference between the interior and exterior angles of a quadrilateral.
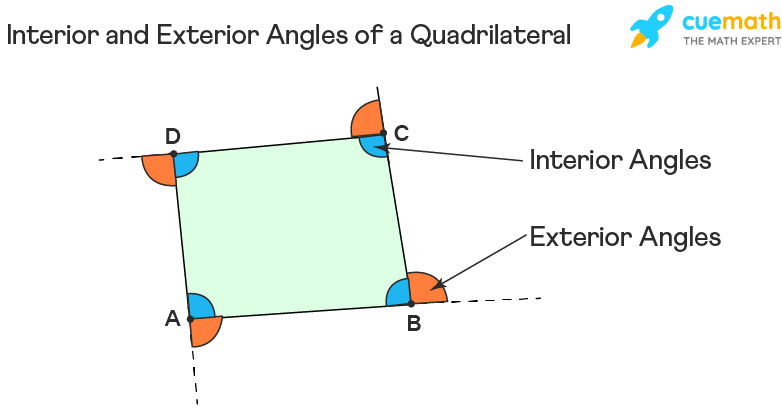
Interior Angles of a Quadrilateral
The angles that lie inside a quadrilateral are called its interior angles. The sum of the interior angles of a quadrilateral is 360°. This helps in calculating the unknown angles of a quadrilateral. In case if the quadrilateral is a square or a rectangle, then we know that all its interior angles are 90° each.
Example: Find the 4th interior angle of a quadrilateral if the other 3 angles are 85°, 90°, and 65° respectively.
Solution:
Using the angle sum property of quadrilaterals, we can find the unknown angles of quadrilateral.
So, 85° + 90°+ 65° = 240. We know that the sum of the interior angles of a quadrilateral is 360°. Therefore, the 4th angle = 360 - 240 = 120°
Exterior Angles of a Quadrilateral
The angles that are formed between one side of a quadrilateral and another line extended from an adjacent side are called its exterior angles. If we observe the figure given above, we can see that the exterior angle and interior angle form a straight line, and hence, they make a linear pair. Therefore, if one interior angle of a quadrilateral is known, we can find the value of its corresponding exterior angle. For example, if an interior angle of a quadrilateral is 60°, then its corresponding exterior angle will be, 180 - 60 = 120°. In case, if the quadrilateral is a square or a rectangle, then all its exterior angles will be 90° each.
Angles of Quadrilateral Formula
There are some basic formulas related to the interior and exterior angles of a quadrilateral.
- Exterior angle = 180° - Interior angle. This formula is used when an interior angle of a quadrilateral is known and the value of the corresponding exterior angle is required. Since both of them form a linear pair they are supplementary, that is, their sum is always equal to 180°. This formula can also be used to find the interior angle if the corresponding exterior angle is given. In that case, the formula will be, Interior angle = 180° - Exterior angle.
- If 3 angles of a quadrilateral are known, then the 4th angle can be calculated using the formula: 360 - (Sum of the other 3 interior angles)
- The sum of interior angles of a quadrilateral = Sum = (n − 2) × 180°, where 'n' represents the number of sides of the given polygon. In a quadrilateral, n = 4, so after substituting the value of n as 4, we get, Sum = (4 − 2) × 180° = 360°
Angles of Quadrilateral Inscribed in a Circle
When a quadrilateral is inscribed in a circle, it is known as a cyclic quadrilateral. A cyclic quadrilateral is a quadrilateral that lies inside a circle and all its vertices touch the circle. There are many theorems related to the angles of quadrilateral inscribed in a circle. For example, one theorem related to the opposite angles of a cyclic quadrilateral says that," The opposite angles in a cyclic quadrilateral are supplementary, i.e., the sum of the opposite angles is equal to 180°". Observe the following figure which shows that the opposite angles in a cyclic quadrilateral sum up to 180°.

Related Links
Check out the following pages related to the angles of quadrilateral.
Examples on Angles of Quadrilateral
-
Example 1: Find the exterior angle of a quadrilateral if its corresponding interior angle is 68°.
Solution:
We know that the interior and exterior angles of quadrilateral form a linear pair. Using the formula for the exterior angle of a quadrilateral, we will solve the question.
Exterior angle = 180 - Interior angle
Exterior angle = 180 - 68 = 112°. Therefore, the exterior angle is 112°.
-
Example 2: If 3 interior angles of a quadrilateral are given as 77°, 98°, and 110°, find the 4th angle.
Solution: The 4th angle of the quadrilateral can be calculated using the formula: 360 - (Sum of the other 3 interior angles)
Unknown 4th angle = 360 - (Sum of the other 3 interior angles)
Unknown 4th angle = 360 - (77° + 98°+ 110°)
4th angle = 360 - (77° + 98°+ 110°) = 75°

FAQS on Angles of Quadrilateral
What is the Formula for Angles of Quadrilateral?
There are some basic formulas related to the interior and exterior angles of a quadrilateral.
- Exterior angle = 180° - Interior angle. This formula is used when an interior angle of a quadrilateral is known and the value of the corresponding exterior angle is required. Since both of them form a linear pair, their sum is always equal to 180°. This formula can also be used to find the interior angle if the corresponding exterior angle is given. In that case, the formula will be, Interior angle = 180° - Exterior angle.
- If 3 angles of a quadrilateral are known, then the 4th angle can be calculated using the formula: 360 - (Sum of the other 3 interior angles)
- The sum of the interior angles of a quadrilateral = Sum = (n − 2) × 180°, where 'n' represents the number of sides of the given polygon. In a quadrilateral, n = 4, so after substituting the value of n as 4, we get, Sum = (4 − 2) × 180° = 360°
What is the Sum of Interior Angles of Quadrilateral?
According to the angle sum property of quadrilaterals, the sum of the interior angles of a quadrilateral is 360°. This property is useful if 3 angles of a quadrilateral are known, and we need to find the 4th angle. The 4th unknown angle can be calculated by subtracting the sum of the given interior angles from 360.
What are the Adjacent Angles of a Quadrilateral?
The adjacent angles of a quadrilateral are also known as consecutive angles. These angles share a common arm and lie next to each other.
What are the Opposite Angles of a Cyclic Quadrilateral?
The opposite angles of a cyclic quadrilateral are always supplementary. When a quadrilateral is inscribed in a circle, it is known as a cyclic quadrilateral. The opposite angles are those angles that are diagonally opposite to each other. The theorem related to the opposite angles of a cyclic quadrilateral says that," The opposite angles in a cyclic quadrilateral are supplementary, i.e., the sum of the opposite angles is equal to 180°".
How to Find the Interior Angles of a Quadrilateral?
According to the Angle sum property of quadrilaterals, the sum of the interior angles is 360°. Using this property, the unknown angle of a quadrilateral can be calculated if the other 3 sides are given. For example, if 3 angles of a quadrilateral are given as 67°, 87°, and 89°, we can find the 4th angle using the sum of the interior angles. First, we will add the given angles, 67° + 87° + 89° = 243°. Now, we will subtract this sum from 360°, that is, 360° - 243° = 117°. Therefore, the 4th interior angle is 117°.
How to Find the Exterior Angles of a Quadrilateral?
An exterior angle is the angle that is formed between one side of a quadrilateral and another line extended from an adjacent side of the quadrilateral. We know that the exterior angle and the corresponding interior angle of a quadrilateral form a linear pair. Therefore, if one interior angle of a quadrilateral is known, we can find the value of its corresponding exterior angle. For example, if an interior angle of a quadrilateral is 50°, then its corresponding exterior angle will be, 180 - 50 = 130°.
What is the Sum of all Exterior Angles of a Quadrilateral?
The sum of all the exterior angles of a quadrilateral is 360°. This property applies to all convex polygons which means that the sum of exterior angles of all convex polygons is always 360°.
What do the Angles of a Quadrilateral Add Up to?
The interior angles of a quadrilateral add up to 360°. This value is calculated from the formula given by the angle sum property of polygons. Sum of interior angles = (n − 2) × 180°, where 'n' represents the number of sides of the given polygon. In this case, n = 4. Therefore, after substituting the value of n as 4, the sum is = (4 − 2) × 180° = 360°.
visual curriculum
