Angles of a Parallelogram
There are four interior angles in a parallelogram and the sum of the interior angles of a parallelogram is always 360°. The opposite angles of a parallelogram are equal and the consecutive angles of a parallelogram are supplementary. Let us read more about the properties of the angles of a parallelogram in detail.
| 1. | Properties of Angles of a Parallelogram |
| 2. | Theorems Related to Angles of a Parallelogram |
| 3. | FAQs on Angles of a Parallelogram |
Properties of Angles of a Parallelogram
A parallelogram is a quadrilateral with equal and parallel opposite sides. There are some special properties of a parallelogram that make it different from the other quadrilaterals. Observe the following parallelogram to relate to its properties given below:

- The opposite angles of a parallelogram are congruent (equal). Here, ∠A = ∠C; ∠D = ∠B.
- All the angles of a parallelogram add up to 360°. Here,∠A + ∠B + ∠C + ∠D = 360°.
- All the respective consecutive angles are supplementary. Here, ∠A + ∠B = 180°; ∠B + ∠C = 180°; ∠C + ∠D = 180°; ∠D + ∠A = 180°
Theorems Related to Angles of a Parallelogram
The theorems related to the angles of a parallelogram are helpful to solve the problems related to a parallelogram. Two of the important theorems are given below:
- The opposite angles of a parallelogram are equal.
- Consecutive angles of a parallelogram are supplementary.
Let us learn about these two special theorems of a parallelogram in detail.
Opposite Angles of a Parallelogram are Equal
Theorem: In a parallelogram, the opposite angles are equal.
Given: ABCD is a parallelogram, with four angles ∠A, ∠B, ∠C, ∠D respectively.
To Prove: ∠A =∠C and ∠B=∠D
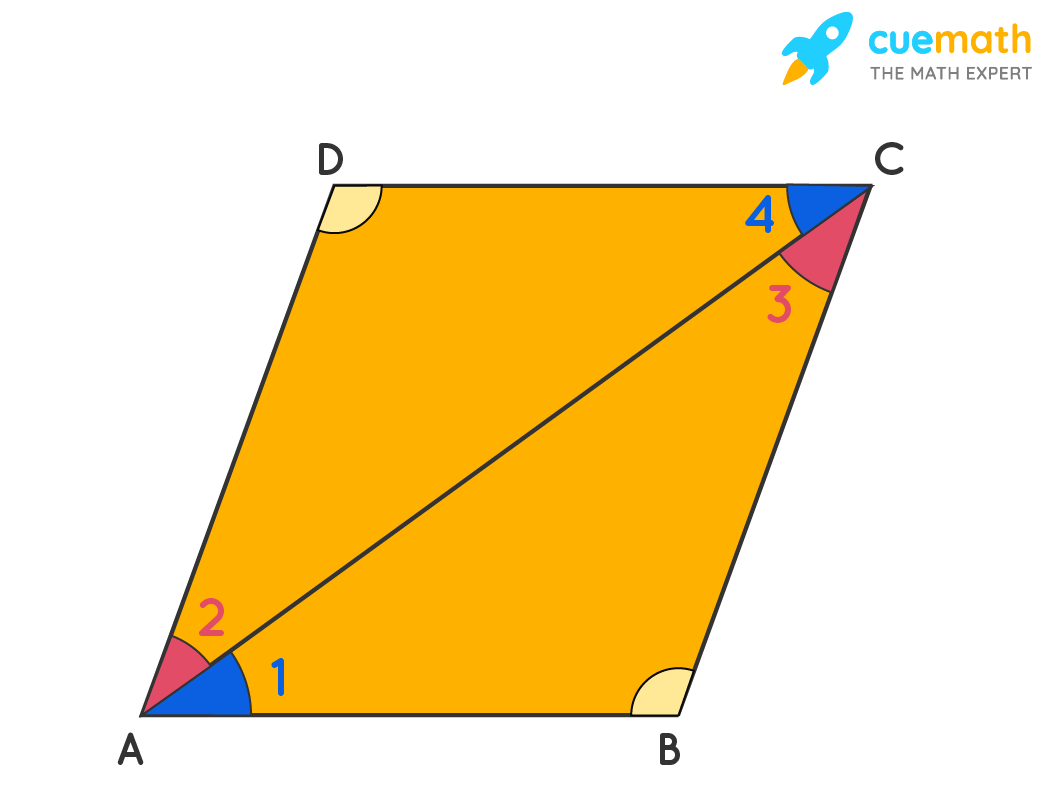
Proof: In the parallelogram ABCD, diagonal AC is dividing the parallelogram into two triangles. On comparing triangles ABC, and ADC. Here we have:
AC = AC (common sides)
∠1 = ∠4 (alternate interior angles)
∠2 = ∠3 (alternate interior angles)
Thus, the two triangles are congruent, △ABC ≅ △ADC
This gives ∠B = ∠D by CPCT (corresponding parts of congruent triangles).
Similarly, we can show that ∠A =∠C.
Hence proved, that opposite angles in any parallelogram are equal.
The converse of the above theorem says if the opposite angles of a quadrilateral are equal, then it is a parallelogram. Let us prove the same.
Given: ∠A =∠C and ∠B=∠D in the quadrilateral ABCD.
To Prove: ABCD is a parallelogram.
Proof:
The sum of all the four angles of this quadrilateral is equal to 360°.
= [∠A + ∠B + ∠C + ∠D = 360º]
= 2(∠A + ∠B) = 360º (We can substitute ∠C with ∠A and ∠D with ∠B since it is given that ∠A =∠C and ∠B =∠D)
= ∠A + ∠B = 180º . This shows that the consecutive angles are supplementary. Hence, it means that AD || BC. Similarly, we can show that AB || CD.
Hence, AD || BC, and AB || CD.
Therefore ABCD is a parallelogram.
Consecutive Angles of a Parallelogram are Supplementary
The consecutive angles of a parallelogram are supplementary. Let us prove this property considering the following given fact and using the same figure.

Given: ABCD is a parallelogram, with four angles ∠A, ∠B, ∠C, ∠D respectively.
To prove: ∠A + ∠B = 180°, ∠C + ∠D = 180°.
Proof: If AD is considered to be a transversal and AB || CD.
According to the property of transversal, we know that the interior angles on the same side of a transversal are supplementary.
Therefore, ∠A + ∠D = 180°.
Similarly,
∠B + ∠C = 180°
∠C + ∠D = 180°
∠A + ∠B = 180°
Therefore, the sum of the respective two adjacent angles of a parallelogram is equal to 180°.
Hence, it is proved that the consecutive angles of a parallelogram are supplementary.
Related Articles on Angles of a Parallelogram
Check out the interesting articles given below that are related to the angles of a parallelogram.
Solved Examples on Angles of a Parallelogram
-
Example 1: One angle of a parallelogram measures 75°. Find the measure of its adjacent angle and the measure of all the remaining angles of the parallelogram.
Solution:
Given that one angle of a parallelogram = 75°
Let the adjacent angle be x
We know that the consecutive (adjacent) angles of a parallelogram are supplementary.
Therefore, 75° + x° = 180°
x = 180° - 75° = 105°
To find the measure of all the four angles of a parallelogram we know that the opposite angles of a parallelogram are congruent.
Hence, ∠1 = 75°, ∠2 = 105°, ∠3 = 75°, ∠4 = 105° -
Example 2: The values of the opposite angles of a parallelogram are given as follows: ∠1 = 75°, ∠3 = (x + 30)°, find the value of x.
Given: ∠1 and ∠3 are opposite angles of a parallelogram.Solution:
Given: ∠1 = 75° and ∠3 = (x + 30)°
We know that the opposite angles of a parallelogram are equal.
Therefore,
(x + 30)° = 75°
x = 75° - 30°
x = 45°
Hence, the value of x is 45°.

FAQs on Angles of a Parallelogram
Do Angles in a Parallelogram add up to 360°?
Yes, all the interior angles of a parallelogram add up to 360°. For example, in a parallelogram ABCD, ∠A + ∠B + ∠C + ∠D = 360°. According to the angle sum property of polygons, the sum of the interior angles in a polygon can be calculated with the help of the number of triangles that can be formed inside it. In this case, a parallelogram consists of 2 triangles, so, the sum of the interior angles is 360°. This can also be calculated by the formula, S = (n − 2) × 180°, where 'n' represents the number of sides in the polygon. Here, 'n' = 4. Therefore, the sum of the interior angles of a parallelogram = S = (4 − 2) × 180° = (4 − 2) × 180° = 2 × 180° = 360°.
What is the Relationship Between the Adjacent Angles of a Parallelogram?
The adjacent angles of a parallelogram are also known as consecutive angles and they are always supplementary (180°).
How are the Opposite Angles of a Parallelogram Related?
The opposite angles of a parallelogram are always equal, whereas, the adjacent angles of a parallelogram are always supplementary.
How to Find the Missing Angles of a Parallelogram?
We can easily find the missing angles of a parallelogram with the help of three special properties:
- The opposite angles of a parallelogram are congruent.
- The consecutive angles of a parallelogram are supplementary.
- The sum of all the angles of a parallelogram is equal to 360°.
What are the Interior Angles of a Parallelogram?
The angles made on the inside of a parallelogram and formed by each pair of adjacent sides are its interior angles. The interior angles of a parallelogram sum up to 360° and any two adjacent (consecutive) angles of a parallelogram are supplementary.
Are all Angles in a Parallelogram Equal?
No, all the angles of a parallelogram are not equal. There are two basic theorems related to the angles of a parallelogram which state that the opposite angles of a parallelogram are equal and the consecutive (adjacent) angles are supplementary.
What is the Sum of the Interior Angles of a Parallelogram?
The sum of the interior angles of a parallelogram is always 360°. According to the angle sum property of polygons, the sum of the interior angles of a polygon can be found by the formula, S = (n − 2) × 180°, where 'n' shows the number of sides in the polygon. In this case, 'n' = 4. Therefore, the sum of the interior angles of a parallelogram = S = (4 − 2) × 180° = (4 − 2) × 180° = 2 × 180° = 360°.
Are the Angles of a Parallelogram 90 Degrees?
In some parallelograms like rectangles and squares, all the angles measure 90°. However, the angles in the other parallelograms may not necessarily be 90°.
Are the Opposite Angles of a Parallelogram Congruent?
Yes, the opposite angles of a parallelogram are congruent. However, the adjacent angles of a parallelogram are always supplementary.
Are Consecutive Angles of a Parallelogram Congruent?
No, the consecutive (adjacent) angles of a parallelogram are not congruent, they are supplementary.
Are the Opposite Angles of a Parallelogram Supplementary?
No, according to the theorems based on the angles of a parallelogram, the opposite angles are not supplementary, they are equal.
math program
math program
visual curriculum
