Adjacent Angles of a Parallelogram
The adjacent angles of a parallelogram are also known as the Consecutive angles of a parallelogram that lie next to each other. There are 4 pairs of adjacent angles in a parallelogram and they are supplementary. Let us learn more about the adjacent angles of a parallelogram in this page.
What are the Adjacent Angles of a Parallelogram?
The adjacent angles of a parallelogram are those angles that are placed next to each other in order. Observe the following parallelogram to see the 4 pairs of adjacent angles. These angles are also known as consecutive angles of a parallelogram. Each pair of adjacent angles here sums up to 180°. The 4 pairs of adjacent angles in the parallelogram are, ∠P and ∠Q, ∠Q and ∠R, ∠R and ∠S, and ∠S and ∠P.
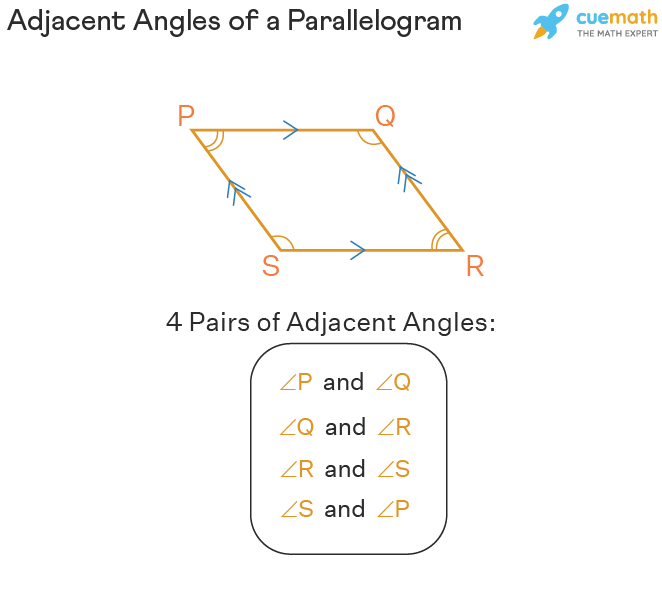
Properties of the Adjacent Angles of a Parallelogram
The properties of the adjacent angles of a parallelogram are as follows:
- The adjacent angles of a parallelogram are supplementary.
- There are 4 pairs of adjacent angles in a parallelogram.
- If the adjacent angles of a parallelogram are equal, that means the parallelogram is a rectangle, and if the sides are also equal, then, it is a square.
Two Adjacent Angles of a Parallelogram are Supplementary
Two adjacent angles of a parallelogram are always supplementary. This means these consecutive angles add up to 180°. Let us understand this fact with the help of the following proof. Observe the following figure to relate to the proof given below.
Proof:
If ABCD is a parallelogram, we know that the opposite sides are parallel.
- Let us take AB || DC in which AD and BC will become the transversals.
- When two parallel lines are cut by a transversal, the co-interior angles on the same side of the transversal are supplementary. In this case, ∠A + ∠D = 180°, and ∠B + ∠C = 180°
- Now, if we take AD || BC, then AB and DC become the transversals. Since the co-interior angles in two parallel lines are supplementary, in this case, ∠A + ∠B = 180°, and ∠D + ∠C = 180°
- Therefore, the sum of any two adjacent angles is supplementary. This means, ∠A + ∠B = 180°, ∠B + ∠C = 180°, ∠C + ∠D = 180°, and ∠D + ∠A = 180°.
☛ Related Articles
Examples on Adjacent Angles of a Parallelogram
-
Example 2: Observe the figure given below and find the value of 'a'.
Solution: It is given that ∠W = (a - 20)° and ∠Z = 115°. We know that the adjacent angles of a parallelogram are supplementary. Therefore, ∠W + ∠Z = 180°. On substituting the given values, we get, a - 20 + 115 = 180. Now, we can find the value of 'a' by solving the equation. That means, a + 95 = 180, so, a = 85.
FAQS on Adjacent Angles of a Parallelogram
What are the Adjacent Angles of a Parallelogram?
The adjacent angles of a parallelogram are the angles that are located next to each other. They are also known as the consecutive angles of a parallelogram. The sum of the adjacent angles of a parallelogram is always supplementary. There are 4 pairs of adjacent angles in a parallelogram.
Are the Adjacent Angles of a Parallelogram Congruent?
No, the adjacent angles of a parallelogram are not congruent, they are supplementary, that is, they sum up to 180°. However, the opposite angles of a parallelogram are congruent.
What is the Relationship Between the Adjacent Angles of a Parallelogram?
The adjacent angles of a parallelogram always sum up to 180°. This means if we know the value of one angle of a parallelogram, then its adjacent angle can be calculated by subtracting it from 180°.
How to Find the Adjacent Angles of a Parallelogram?
The adjacent angles of a parallelogram can be calculated if the other angles are known. Sometimes, the value of 3 angles of a parallelogram is known, in that case, the value of the missing angle can be calculated using the property of the adjacent angles of a parallelogram. The sum of two adjacent angles of a parallelogram is equal to 180°.
If the Adjacent Angles of a Parallelogram are 2x - 4 and 3x - 1, Find the Measure of both the Angles.
If the adjacent angles of a parallelogram are given as (2x -4) and (3x - 1), let us calculate the value of x using the following steps.
- Step 1: Since the adjacent angles of a parallelogram are supplementary, we can write it as, (2x - 4) + (3x - 1) = 180.
- Step 2: Solving this, we get, 5x - 5 = 180. It gives the value of x as, 37. Now, after substituting the value of x as 37 in (2x - 4), we get, (2 × 37) - 4 = 74 - 4 = 70°.
- Step 3: Similarly, the value of the other angle can be calculated by substituting the value of x = 37 in 3x - 1. This means, 3x - 1 = (3 × 37) - 1 = 110°.
- Step 4: Therefore, these two adjacent angles are 70° and 110°, and it can be verified that they sum up to 180°, that is, 70 + 110 = 180°.
Are the Consecutive Angles of a Parallelogram Complementary?
No, the consecutive angles of a parallelogram are not complementary angles. The consecutive angles of a parallelogram are also referred to as the adjacent angles that are supplementary, that is, they add up to 180°.