Disk Method Formula
The disk method is used when the axis of revolution is the boundary of the plane region and the cross-sectional area is perpendicular to the axis of revolution. This method is used to find the volume by revolving the curve \(y=f(x)\) about \(x\)-axis and \(y\)-axis. We call it as Disk Method because the cross-sectional area forms circles, that is, disks. The volume of each disk is the product of its area and thickness.
Let us learn the disk method formula with a few solved examples.

What is the Disk Method Formula?
Let \(R_{1}\) be the region bounded by \(y=f(x)\), \(x=a\), \(x=b\) and \(y=0\). Suppose we form a solid by revolving it around the \(x\)-axis. The volume of the solid is given by:
\[V=\pi\:\int_{a}^{b}\!\![f(x)]^2 dx\]
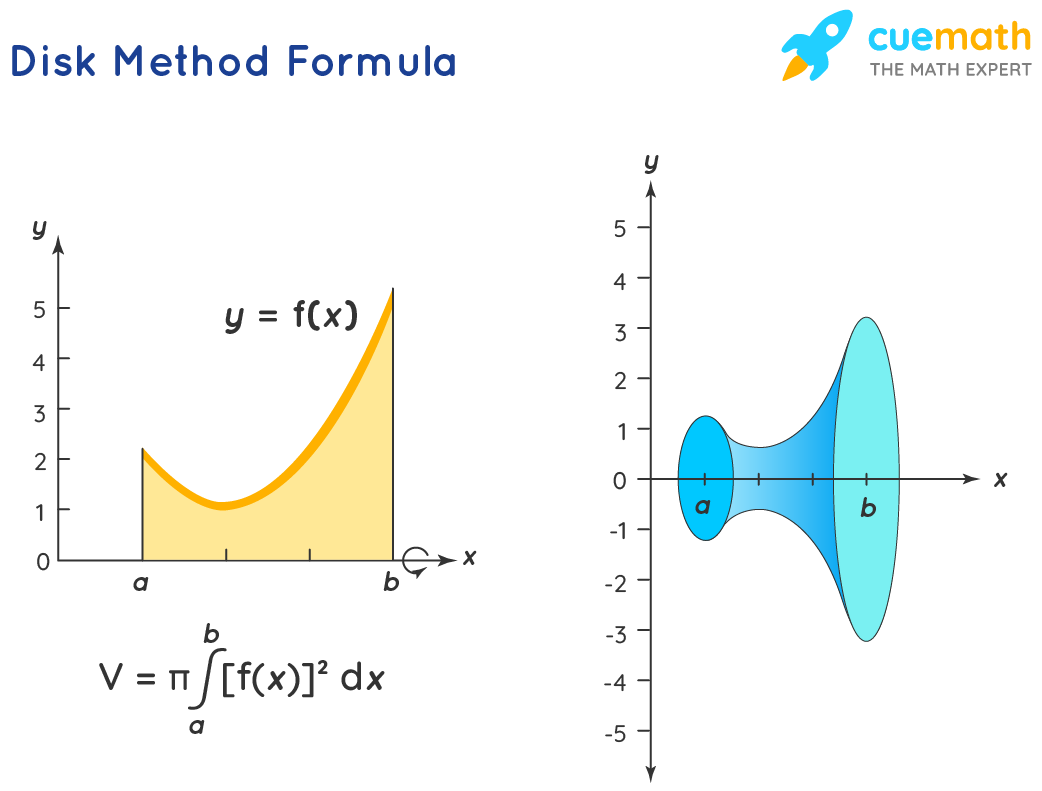
Let \(R_{2}\) be the region bounded by \(x=f(y)\), \(y=c\), \(y=d\) and \(x=0\). Suppose we form a solid by revolving it around the \(y\)-axis.
The volume of the solid is given by:
\[V= \pi\:\int_{c}^{d}\!\! [f(y)]^2 dy\]

Solved Examples on Disk Method Formula
-
Example 1:
Let \(R\) be a region bounded by \(y=x^2\), \(x=-2\), \(x=3\) and \(x\)-axis. Find the volume of the solid obtained by rotating the region \(R\) about \(x\)-axis.
Solution:

The volume is given by
\(\begin{align}V&=\int_{-2}^{3} {\pi (x^2)^2}dx\\&=\pi \int_{-2}^{3} {x^4}dx\\&=\pi\left[\frac{x^5}{5}\right]_{-2}^{3}\\&=55 \pi\end{align}\)
Hence, the required volume is \(55 \pi\). -
Example 2:
Let \(R\) be a region bounded by \(y=x^2-4x+5\), \(x=1\), \(x=4\) and the \(x\)-axis. Find the volume of the solid obtained by rotating the region \(R\) about \(x\)-axis.
Solution:

The volume is given by
\(\begin{align}V&=\pi \int_{1}^{4} {(x^2-4x+5)^2}dx\\&=\pi \int_{1}^{4} {(x^4-8x^3+26x^2-40x+25)}dx\\&=\pi\left[\frac{x^5}{5}-2x^4+\frac{26x^3}{3}-20x^2+25x\right]_{1}^{4}\\&=\frac{78\pi}{5}\end{align}\)
Hence, the required volume is \(\frac{78\pi}{5}\).
visual curriculum