Probability Density Function
Probability density function is a function that provides the likelihood that the value of a random variable will fall between a certain range of values. We use the probability density function in the case of continuous random variables. For discrete random variables, we use the probability mass function which is analogous to the probability density function.
The graph of a probability density function is in the form of a bell curve. The area that lies between any two specified values gives the probability of the outcome of the designated observation. We solve the integral of this function to determine the probabilities associated with a continuous random variable. In this article, we will do a detailed analysis of the probability density function and take a look at the various aspects related to it.
What is Probability Density Function?
Probability density function and cumulative distribution function are used to define the distribution of continuous random variables. If we differentiate the cumulative distribution function of a continuous random variable it results in the probability density function. Conversely, on integrating the probability density function we get the cumulative distribution function.
Probability Density Function Definition
Probability density function defines the density of the probability that a continuous random variable will lie within a particular range of values. To determine this probability, we integrate the probability density function between two specified points.
Probability Density Function Example
Say we have a continuous random variable whose probability density function is given by f(x) = (x + 2)/6, when 0 < x ≤ 2. We want to find P(0.5 < X < 1). Then we integrate (x + 2)/6 within the limits 0.5 and 1. This gives us 0.229. Thus, the probability that the continuous random variable lies between 0.5 and 1 is 0.229.
Probability Density Function Formula
The probability density function of a continuous random variable is analogous to the probability mass function of a discrete random variable. Discrete random variables can be evaluated at a particular point while continuous random variables have to be evaluated between a certain interval. This is because the probability that a continuous random variable will take an exact value is 0. Given below are the various probability density function formulas.
Probability Density Function of Continuous Random Variable
Suppose we have a continuous random variable, X. Let F(x) be the cumulative distribution function of X. Then the formula for the probability density function, f(x), is given as follows:
f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm{d} x}\) = F'(x)
If we want to find the probability that X lies between lower limit 'a' and upper limit 'b' then using the probability density function this can be given as:
P(a < X ≤ b) = F(b) - F(a) = \(\int_{a}^{b}f(x)dx\)
Here, F(b) and F(a) represent the cumulative distribution function at b and a respectively.
Probability Density Function of Normal Distribution
Normal distribution is the most widely used type of continuous probability distribution. The notation for normal distribution is given as \(X \sim N(\mu ,\sigma ^{2})\). The probability density function of a normal distribution is given below.
f(x) = \(\frac{1}{\sigma \sqrt{2\Pi}}e^{\frac{-1}{2}\left ( \frac{x - \mu }{\sigma } \right )^{2}}\)
Here, \(\mu\) is the mean and \(\sigma\) is the standard deviation while \(\sigma\)2 is the variance.
Probability Density Function Graph
If X is a continuous random variable then the probability distribution of this variable is given by the probability density function. The graph given below depicts the probability that X will lie between two points a and b.
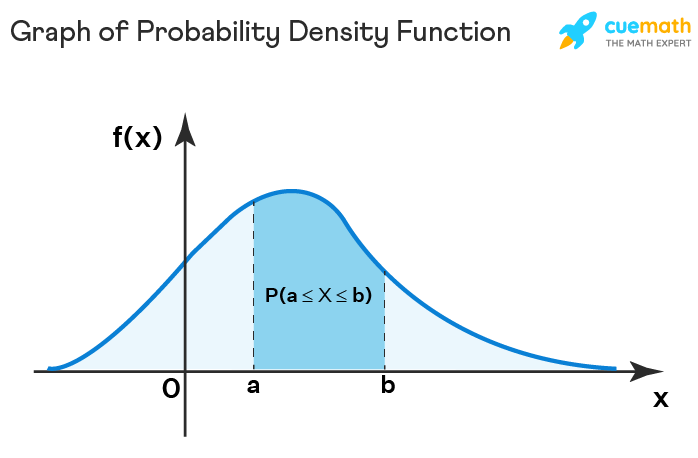
Mean of Probability Density Function
In the case of a probability density function, the mean is the expected value or the average value of the random variable. If f(x) is the probability density function of the random variable X, then mean is given by the following formula:
E[X] = \(\mu = \int_{-\infty }^{\infty}xf(x)dx\)
Median of Probability Density Function
The median is the value that splits the probability density function curve into two equal halves. Suppose x = m is the value of the median. The area under the curve from \(-\infty\) to m will be equal to the area under the curve from m to \(\infty\). This implies that the value of the median is 1 / 2. Thus, the median of the probability density function is given as follows:
\(\int_{-\infty }^{m}f(x)dx = \int_{m}^{\infty }f(x)dx\) = 1/2

Variance of Probability Density Function
The expected value of the squared deviation from the mean is the variance of a random variable. Expressing this definition mathematically we get,
Var(X) = \(E[(X - \mu )^{2}]\)
To represent this variance with the help of the probability density function, the formula is given as:
Var(X) = \(\sigma ^{2} = \int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\)
Properties of Probability Density Function
The properties of the probability density function help to solve questions faster. If f(x) is the probability distribution of a continuous random variable, X, then some of the useful properties are listed below:
- f(x) ≥ 0. This implies that the probability density function for all real numbers can be either equal to or greater than 0. But it can never be negative or lesser than 0.
- \(\int_{-\infty }^{\infty}f(x)dx\) = 1. Thus, the total area under the probability density curve will be equal to 1.
Related Articles:
Important Notes on Probability Density Function
- Probability density function determines the probability that a continuous random variable will fall between a range of specified values.
- On differentiating the cumulative distribution function, we obtain the probability density function.
- The mean of the probability density function can be give as E[X] = \(\mu = \int_{-\infty }^{\infty}xf(x)dx\).
- As the median divides the probability density function curve into 2 equal halves, its value will be equal to 1 / 2.
- The variance of a probability density function is given by Var(X) = \(\sigma ^{2} = \int_{-\infty }^{\infty }(x - \mu )^{2}f(x)dx\)
Examples on Probability Density Function
-
Example 1: If the probability density function is given as:
f(x) = \(\left\{\begin{matrix} x(x-1) &0\leq x < 3 \\ x& x\geq3 \end{matrix}\right.\)
Find P(1< X < 2).
Solution: Integrating the function,
\(\int_{1}^{2}x(x-1)dx\) = \(\int_{1}^{2}(x^{2}-x)dx\)
= \([\frac{x^{3}}{3} - \frac{x^{2}}{2}]_{1}^{2}\)
= 5 / 6
Answer: P(1< X < 2) = 5 / 6 -
Example 2: If X is a continuous random variable with the probability density function given as:
f(x) = \(\left\{\begin{matrix} \frac{be^{-x}}{2} & x\geq 0\\ 0 & \text{otherwise} \end{matrix}\right.\)
Find the value of b.
Solution: We know from properties of probability density function that \(\int_{-\infty }^{\infty}f(x)dx\) = 1
\(\int_{0}^{\infty }\frac{be^{-x}}{2}dx\) = 1
On integrating,
\(\frac{b}{2}\left [ -e^{-x} \right ]_{0}^{\infty }\) = 1
b / 2 = 1
b = 2
Answer: b = 2 -
Example 3: Find the expected value of X if the probability density function is defined as:
f(x) = \(\left\{\begin{matrix} \frac{3}{2}x^{2} & 0\leq x\leq 2\\ 0& \text{otherwise} \end{matrix}\right.\)
Solution: We know that, E[X] = \(\int_{-\infty }^{\infty}xf(x)dx\)
= \(\int_{-\infty }^{0}x(0)dx + \int_{0}^{2}x (\frac{3x^{2}}{2})dx + \int_{2}^{\infty }x(0)dx\)
= \(\frac{3}{2}[\frac{x^{4}}{4}]_{0}^{2}\)
= (3/8) [16]
= 6
Answer: Mean = 6

FAQs on Probability Density Function
What is Meant by the Probability Density Function?
Probability density function is a function that is used to give the probability that a continuous random variable will fall within a specified interval. The integral of the probability density function is used to give this probability.
What is the Probability Density Function Formula?
We can differentiate the cumulative distribution function (cdf) to get the probability density function (pdf). This can be given by the formula f(x) = \(\frac{\mathrm{d} F(x)}{\mathrm{d} x}\) = F'(x). Here, f(x) is the pdf and F'(x) is the cdf.
How to Calculate the Probability Density Function?
To calculate the probability density function we differentiate the cumulative distribution function. If we integrate the probability density function, we get the probability that a continuous random variable lies within a certain interval.
How to Find the Mean of Probability Density Function?
The expected value is also known as the mean. The mean of the probability density function is given by the formula \(\mu = \int_{-\infty }^{\infty}xf(x)dx\).
Is Probability Density Function Always Positive?
The value of the integral of a probability density function will always be positive. This is because probability can never be negative hence, as a consequence, the probability density function can also never be negative.
How Do You Find the Probability of a Probability Density Function?
To find the probability that a continuous random variable X, falls between an interval a and b we use the probability density function, f(x). This formula is given as P(a < X < b) = \(\int_{a}^{b}f(x)dx\)
What are the Features of Probability Density Function?
The features of the probability density function are given below:
- The probability density function will always be a positive value.
- The total area under the probability density function curve will always be equal to 1.
visual curriculum
