Average Rate of Change Calculator

Average Rate of Change Calculator calculates the average rate of change for the given function. The average rate at which one quantity is changing with respect to another is described by the average rate of change.

What is the Average Rate of Change Calculator?

Average Rate of Change Calculator is an online tool that helps to calculate how much the given function changes within a particular interval. If we divide the output by the input we can determine the average rate of change. To use this average rate of change calculator, enter the values in the given input boxes.

Average Rate of Change Calculator

How to Use Average Rate of Change Calculator?

Please follow the steps below to find the average rate of change using the online average rate of change calculator:

• Step 1: Go to Cuemath’s online average rate of change calculator.
• Step 2: Enter the values in the given input boxes of the average rate of change calculator.
• Step 3: Click on the "Calculate" button to calculate the average rate of change for the given function.
• Step 4: Click on the "Reset" button to clear the fields and enter new values.

How Does Average Rate of Change Calculator Work?

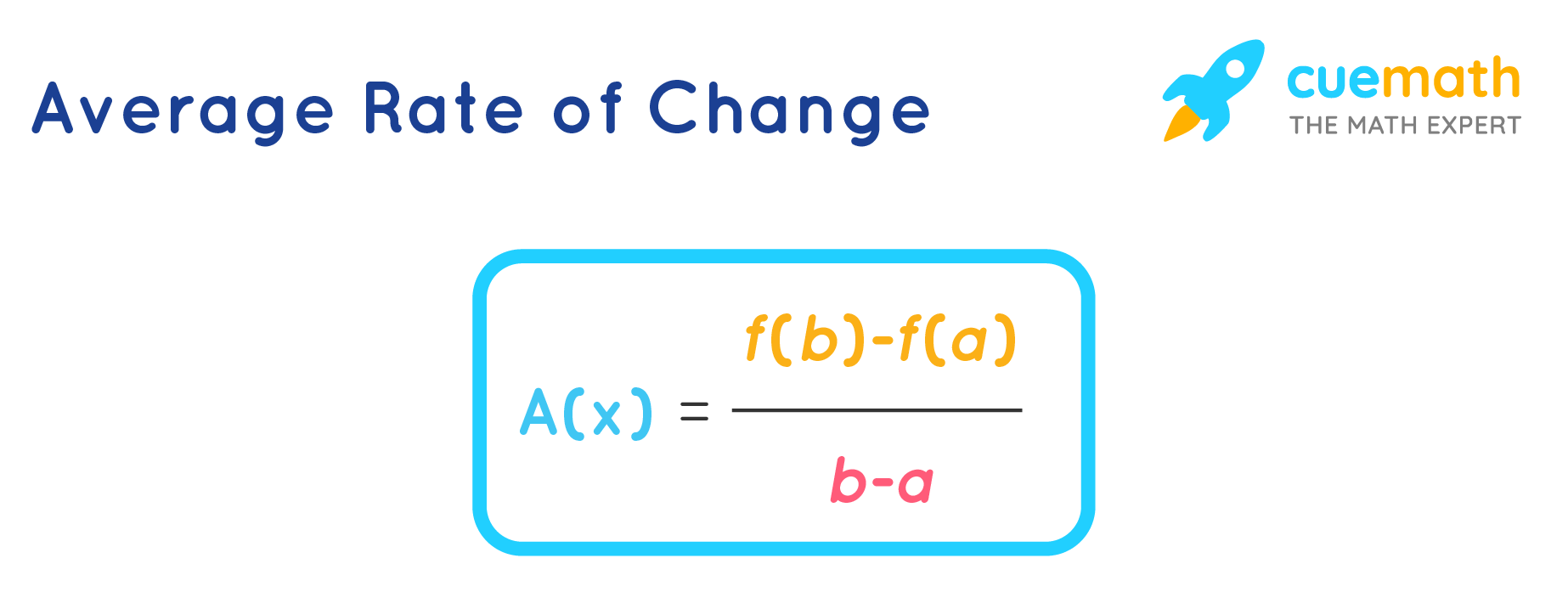
When we want to see how one quantity changes with respect to a change in another quantity, we use the average rate of change formula. Suppose we are given a function, f(x), and we want to determine the average rate of change when the function goes from point 'a' to point 'b'. Then the following steps can be used to do the same:

• Step 1: Find the value of the function at a. This is given by f(a).
• Step 2: Find the value of the function at b. We denote this as f(b).
• Step 3: Subtract f(a) from f(b); f(b) - f(a).
• Step 4: Now subtract the value of a from b; b - a.
• Step 5: We now divide the value obtained in step 3 by the value from step 4. [f(b) - f(a)] / [b - a].
• Step 6: This gives us the average rate of change of the function.

Thus, the formula for the average rate of change, A(x), is given by:

A(x) = [f(b) - f(a)] / [b - a]

Solved Examples on Average Rate of Change

Example 1: Calculate the average rate of change of a function, f(x) = 3x + 5 as x changes from 2 to 5 and verify it using the average rate of change calculator.

Solution:

Given: Function f(x) = 3x + 5, a = 2 and b = 5

f(a) = f(2) = 3(2) + 5 = 11

f(b) = f(5) = 3(5) + 5 = 20

b - a = 5 - 2 = 3

A(x) = [f(b) - f(a)] / (b - a)

= (20 - 11) / (5 - 2)

= 3

Example 2: Calculate the average rate of change of a function, f(x) = 0.2x³ - 2 as x changes from -7 to 3 and verify it using the average rate of change calculator.

Solution:

Given: Function f(x) = 0.2x³ - 2, a = -7 and b = 3

f(a) = f(-7) = 0.2(-7)³ - 2 = -70.6

f(b) = f(3) = 0.2(3)³ - 2 = 3.4

b - a = 3 - (-7) = 10

A(x) = [f(b) - f(a)] / (b - a)

= (3.4 - (-70.6)) / (3 - (-7))

= 7.4

Now, try the average rate of change calculator and find the average rate of change for:

• x³ + 6x + 5, x varies from 5 to 9
• 2x² + 2x + 4, x varies from -2 to -8

☛ Math Calculators: