Asymptote Formula

An asymptote is a straight line with respect to a curve such that it tends to meet the curve at infinity. This can be more clearly understood as a line drawn at a minimum parallel distance to the tangent of a curve, such that it does not cut or touch the curve. Asymptote formula is generally defined, for a hyperbola. Asymptote Formula is represented as an equation of a line.

What is an Asymptote Formula?

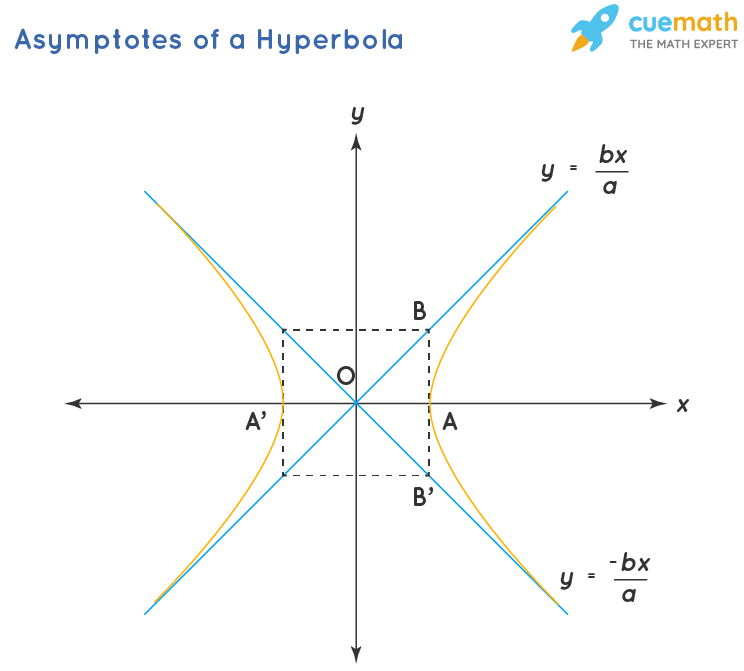
The asymptotes of a hyperbola are a pair of straight lines. The asymptotes of a hyperbola having an equation  x²/a² - y²/b² = 0 is given by the following formula:

Equation of Asymptotes:  y = b/a.x, and y = -b/a.x

Equation of Pair of Asymptotes: x²/a²  - y²/b² = 0

Let us check out a few solved examples to more clearly understand Asymptotes Formula.

Examples Using Asymptote Formula

Example 1: Find the equation of pair of asymptotes of a hyperbola x²/16 - y²/25 = 1.

Solution:

Given equation of the hyperbola is x²/16 - y²/25 = 1

For a hyperbola having an equation x²/a² - y²/b² = 1 the equation of its pair of asymptotes is bx/a and -bx/a

Here it is known that a = 4 and b = 5

Hence the equation of pair of asymptotes is y = 4x/5 and y =-4x/5

Answer: Equation of the pair of aymptotes is 5y-4x = 0 and 5y +4x =0

Example 2: Find the equations of the asymptotes of the hyperbola x²/49 - y²/36 = 1.

Solution:

The given equation of the hyperbola is x²/49 - y²/36 = 1
                                                              x²/7² - y²/6² = 1
Let us compare the above equation with the standard equation of a hyperbola x²/a² - y²/b² = 1
We get a = 7 and b = 6

Further the equations of the asymptotes is y = b/a.x, and y = -b/a.x

y = 6x/7 and y = -6x/7
7y = 6x and 7y = -6x
7y- 6x = 0 and 6x + 7y = 0

Answer: Hence the equations of the asymptotes are   7y- 6x = 0 and 6x + 7y = 0