Arithmetic Sequence Explicit Formula
Arithmetic sequence explicit formula is useful to find any terms of the given arithmetic sequence. An arithmetic sequence is a sequence of numbers in which the differences between any two consecutive numbers are the same. For an arithmetic sequence 2, 5, 8, 11, .... the first term is a = 2, and the common difference is d = 5 - 2 = 3. The arithmetic sequence explicit formula for this series is an = a + (n - 1)d, or an = 2 + (n - 1)3 or an = 3n - 1.
Here the arithmetic sequence explicit formula (an = 3n - 1) is useful to find any terms of the series and can be calculated without knowing the previous term. Let us learn the arithmetic sequence explicit formula, and its derivation with the help of examples, FAQs.
What Is Arithmetic Sequence Explicit Formula?
The arithmetic sequence explicit formula is used to find any term (nth term) of the arithmetic sequence, a1, a2, a3, ..., an,.... using its first term (a) and the common difference (d). This formula gives the nth term formula of an arithmetic sequence. The arithmetic sequence explicit formula is an = a + (n - 1)d.
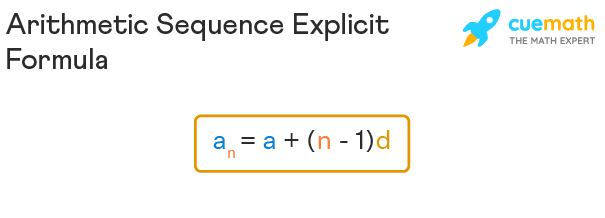
Derivation of Arithmetic Sequence Explicit Formula
The arithmetic sequence explicit formula is derived from the terms of the arithmetic sequence. It helps to easily find any term of the arithmetic sequence. The arithmetic sequence is a1, a2, a3, ..., an. Here the first term is referred as 'a' and we have a = a1 and the common difference is denoted as 'd'. The formula for the common difference is d = a2 - a1 = a3 - a2 = an - an - 1. The nth term of the arithmetic sequence represents the explicit formula of the arithmetic sequence.
Explicit Formula: an= a + (n - 1) d
where,
- \(a_n\) = nth term of the arithmetic sequence
- a = the first term of the arithmetic sequence
- d = the common difference (the difference between every term and its previous term. i.e., d \(=a_n-a_{n-1}\)
Example of Arithmetic Sequence Explicit Formula
An example of an arithmetic sequence is -3, -6, -9, -12, ... , for which the difference between any term and its previous term is -3. This difference is usually termed as the common difference and is denoted by d. The first term of an arithmetic sequence is represented by a1 or a = -3. Applying the formula for the nth term, the arithmetic series explicit formula is an = a + (n - 1)d = -3 + (n - 1)(-3) = -3n + 3 - 3 = -3n, or an = -3n.

Examples Using Arithmetic Sequence Explicit Formula
Example 1: Find the 15th term of the arithmetic sequence -3, -1, 1, 3, ..... using the arithmetic sequence explicit formula.
Solution:
The first term of the given sequence is, a = -3
The common difference is, d = -1 - (-3) (or) 1 - (-1) (or) 3 - 1 = 2.
The 15th term of the given sequence is calculated using,
\(a_n\) = a + (n - 1) d
\(a_{15}\) = -3 + (15 - 1) 2 = -3 + 14(2) = -3 + 28 = 25.
Answer: The 15th term of the given sequence = 25.
Example 2: Find the common difference of the arithmetic sequence whose first term is 1/2 and whose 10th term is 9.
Solution:
The first term is, a = 1/2.
Its 10th term is a\(_{10}\) = 9.
Using the arithmetic sequence explicit formula, we have the following formula.
\(a_n\) = a + (n - 1) d
Substituting n = 10, we get
\(a_{10}=a+(n-1)d\)
9 = (1/2) + (10 - 1) d
9 = (1/2) + 9d
Subtracting 1/2 from both sides,
17/2 = 9d
Dividing both sides by 9,
d = 17/18
Answer: The common difference is 17/18.
Example 3: Find the general term (or) nth term of the arithmetic sequence -1/2, 2, 9/2, .....
Solution:
The first term of the given sequence is, a = -1/2.
The common difference is d = 2 - (-1/2) (or) 9/2 - 2 = 5/2.
We can find the general term (or) nth term of an arithmetic sequence using the arithmetic sequence explicit formula.
\(a_n\) = a + (n - 1) d
\(a_n\) = -1/2 + (n - 1) (5/2)
\(a_n\) = - 1/2 + 5/2 n - 5/2
\(a_n\) = (5/2) n - 3
Answer: The nth term of the given sequence = (5/2) n - 3.
FAQs on Arithmetic Sequence Explicit Formula
What Is Arithmetic Sequence Explicit Formula?
The arithmetic sequence explicit formula is a formula that is used to find the nth term of an arithmetic sequence without computing any other terms before the nth term. Using this formula, the nth term of an arithmetic sequence whose first term is 'a' and common difference is 'd' is, a\(_n\) = a + (n - 1) d.
How To Derive Arithmetic Sequence Explicit Formula?
We know that the differences between every two consecutive terms of an arithmetic sequence are all same. Thus, an arithmetic sequence is of the form a, a + d, a + 2d, .... If we observe here, the 1st term is a = a + (1 - 1) d, the 2nd term is a + d = a + (2 - 1) d, and the 3rd term is a + 2d = a + (3 - 1) d. In the same way, the nth term is, a\(_n\) = a + (n - 1) d.
What Are the Applications of Arithmetic Sequence Explicit Formula?
Using the arithmetic sequence explicit formula, we can find any term of an arithmetic sequence just with the help of the first term and the common difference. For example, to find the 50th term of an arithmetic sequence -7, -5, -3, ..., we just use the first term, a = -7 and the common difference, d = 2 and substitute in the formula a\(_n\) = a + (n - 1) d, then we get a\(_{50}\) = (-7) + (50 - 1) 2 = 91.
What Is the 100th term of the Arithmetic Sequence 1/4, 1/2, 3/4, ... Using Arithmetic Sequence Explicit Formula?
In the given sequence, a = 1/4 and the common difference is, d = 1/2 - 1/4 = 3/4 - 1/2 = ... = 1/4. Substituting n = 100 in the arithmetic sequence explicit formula, we get
a\(_n\) = a + (n - 1) d
a\(_{100}\) = (1/4) + (100 - 1) (1/4) = 25.
visual curriculum
