A day full of math games & activities. Find one near you.

Vector Equations

Vector equations ares used to represent the equation of a line or a plane with the help of the variables x, y, z. The vector equation defines the placement of the line or a plane in the three-dimensional framework. The vector equation of a line is r = a + λb, and the vector equation of a plane is r.n = d.

Let us check the vector equations, and how to find the vector equations of a line or a plane, with the help of examples, FAQs.

1.	What Are Vector Equations?
2.	Vector Equations Of Line
3.	Vector Equations Of Plane
4.	Vector Equations Vs Cartesian Equations
5.	FAQs on Vector Equations

What Are Vector Equations?

Vector equations are used to represent the lines or planes in a three-dimensional framework. The three-dimensional plane requires three coordinates with respect to the three-axis and here the vectors are helpful to easily represent the vector equation of a line or a plane. In a three-dimensional framework the unit vector along the x-axis is \(\hat i \), the unit vector along the y-axis is \(\hat j\), and the unit vector along the z-axis is \(\hat k\). The vector equations are written using \(\hat i\), \(\hat j\), \(\hat k\) and can be represented geometrically in the three-dimensional plane. The simplest form of vector equation of a line is \(\vec r = \vec a + λ\vec b\) and the vector equation of a plane is \(\overrightarrow r. \hat n\) = d.

Vector Equation of a Line: \(\vec r = \vec a + λ\vec b\)

Vector Equation of a Plane: \(\overrightarrow r. \hat n\) = d

There are two methods of finding the vector equations of a line and four methods of finding the vector equations of a plane. Let us check the different vector equations of a line and a plane.

Vector Equations Of Line

Vector equations of a line can be computed with the help of any two points on the line, or with the help of a point on the line and a parallel vector. The two methods of forming a vector form of the equation of a line are as follows.

Vector Equations - Line

The vector equation of a line passing through a point and having a position vector \(\vec a\), and parallel to a vector line \(\vec b\) is \(\vec r = \vec a + λ\vec b\).
The vector equation of a line passing through two points with the position vector \(\vec a\), and \(\vec b\) is \(\vec r = \vec a + λ(\vec b - \vec a)\).

Vector Equations Of Plane

The vector equation of a plane represents a vector form of the equation of a plane in a cartesian coordinate system and can be computed through different methods, based on the available inputs values about the plane. The following are the four different expressions for the equation of a plane in vector form.

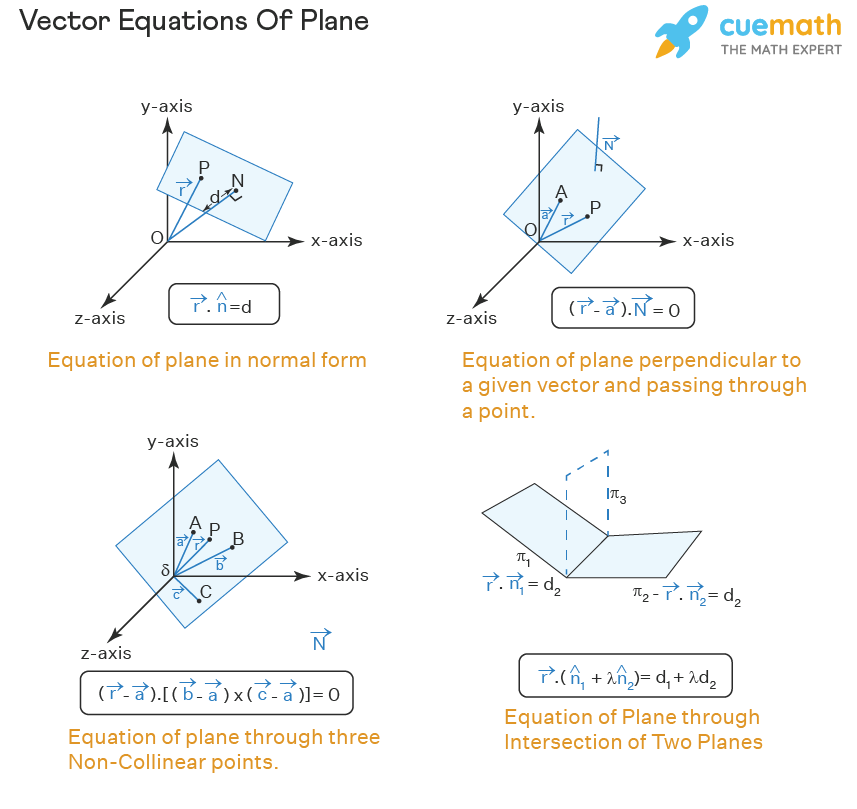
Vector Equations - Plane

Normal Form: Equation of a plane at a perpendicular distance d from the origin and having a unit normal vector \(\hat n \) is \(\overrightarrow r. \hat n\) = d.
Perpendicular to a given Line and through a Point: The equation of a plane perpendicular to a given vector \(\overrightarrow N \), and passing through a point \(\overrightarrow a\) is \((\overrightarrow r - \overrightarrow a). \overrightarrow N = 0\)
Through three Non Collinear Lines: The equation of a plane passing through three non collinear points \(\overrightarrow a\), \(\overrightarrow b\), and \(\overrightarrow c\), is \((\overrightarrow r - \overrightarrow a)[(\overrightarrow b - \overrightarrow a) × (\overrightarrow c - \overrightarrow a)] = 0\).
Intersection of Two Planes: The equation of a plane passing through the intersection of two planes \(\overrightarrow r .\hat n_1 = d_1\), and \(\overrightarrow r.\hat n_2 = d_2 \), is \(\overrightarrow r(\overrightarrow n_1 + λ \overrightarrow n_2) = d_1 + λd_2\).

Vector Equations vs Cartesian Equations

Vector equations can be easily transformed into cartesian equations. The cartesian equations have the variables of x, y, z and it does not have any of the unit vectors of i, j, k in its equations. The cartesian form of the equation is formed by eliminating the constant λ from the vector equations. Let us try to understand the difference between vector equations and cartesian equations.

The vector equation of a line \(\vec r = \vec a + λ\vec b\) which is passing through a point \(\vec a\), and is parallel to a vector \(\vec b\) is transformed into cartesian form by representing \(\vec a = x_1\hat i + y_1\hat j + z_1\hat k\) and \(\vec b = a\hat i + b\hat j + c\hat k\), and the transformed equation in cartesian form is \(\dfrac{x - x_1}{a} = \dfrac{y - y_1}{b} = \dfrac{z - z_1}{c}\).

Similarly, we can write each of the vector equations of a line and a plane into cartesian equation form. The below table shows the transformation of each of the vector equations into a cartesian equation.

Vector Equation	Cartesian Equation
\(\vec r = \vec a + λ\vec b\)	\(\dfrac{x - x_1}{a} = \dfrac{y - y_1}{b} = \dfrac{z - z_1}{c}\)
\(\vec r = \vec a + λ(\vec b - \vec a)\)	\(\dfrac{x - x_1}{x_2 - x_1} = \dfrac{y - y_1}{y_2 - y_1} = \dfrac{z - z_1}{z_2 - z_1}\)
\(\overrightarrow r. \hat n\) = d	lx + ny + nz = d
\((\overrightarrow r - \overrightarrow a). \overrightarrow N = 0\)	A(x - x₁) + B(y - y₁) + C(z - z₁) = 0
\((\overrightarrow r - \overrightarrow a)[(\overrightarrow b - \overrightarrow a) × (\overrightarrow c - \overrightarrow a)] = 0\)	\(\begin{vmatrix}x-x_1&y-y_1&z-z_1\\x_2 - x_1&y_2 - y_1&z_2 - z_1\\x_3 - x_1&y_3 - y_1&z_3 - z_1\end{vmatrix}=0\)
\(\overrightarrow r(\overrightarrow n_1 + λ \overrightarrow n_2) = d_1 + λd_2\)	(A₁x + B₁y + C₁z - d₁) + λ(A₂x + B₂y + C₂z - d₂) = 0

☛ Related Topics

Examples on Vector Equation

Example 1: Find the vector equation of the line passing through the point (3, 5, -2), and is parallel to the vector \(5\hat i + \hat j + 4\hat k \).

Solution:

The given point is (3, 5, -2), and the vector is \(5\hat i + \hat j + 4\hat k \).

These can be represented as \(\vec a = 3\hat i + 5\hat j -2\hat k\), and \(\vec b = 5\hat i + \hat j + 4\hat k \).

The vector equation of a line passing through a point \(\vec a\), and parallel to a vector line \(\vec b\) is \(\vec r = \vec a + λ\vec b\).

\(\vec r = 3\hat i + 5\hat j -2\hat k + λ(5\hat i + \hat j + 4\hat k)\)

Therefore the vector equation of a line passing through a point and is parallel to another vector is \(\vec r = 3\hat i + 5\hat j -2\hat k + λ(5\hat i + \hat j + 4\hat k)\).
Example 2: Find the vector equation of a plane passing through a point (3, 4, 2), and is perpendicular to a line with direction cosines of 2, -3, 1.

Solution:

The coordinates of the point is (3, 4, 2), and the direction cosines of the perpeThe ndicular vector are 2, -3, 1. These can be represented as follows.

The point is represented in vector form as \(\vec a = 3\hat i + 4\hat j + 2\hat k\).

And the normal vector is represented as \(\vec N = 2\hat i -3\hat j + \hat k\).

The required vector equation of the plane is \((\overrightarrow r - \overrightarrow a). \overrightarrow N = 0\). Substituting the values we have the following equation.

\((\overrightarrow r - (3\hat i + 4\hat j + 2\hat k)). (2\hat i -3\hat j + \hat k) = 0\)

Therefore the required vector equation of the plane is \((\overrightarrow r - (3\hat i + 4\hat j + 2\hat k)). (2\hat i -3\hat j + \hat k) = 0\).

go to slide go to slide

Great learning in high school using simple cues

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.

Book a Free Trial Class

Practice Questions on Vector Equation

go to slide go to slide

FAQs on Vector Equations

What Are Vector Equations?

Vector equations are a form of equations represented using the vectors \(\hat i\), \(\hat j\), and \(\hat k\), which are the unit vectors along the x-axis, y-axis, and z-axis respectively. The vector equations of a line are \(\vec r = \vec a + λ\vec b\), and the vector equation of a plane is \(\overrightarrow r. \hat n\) = d.

How To Write A Vector Equation?

The vector equation is written with the help of the vectors \(\hat i\), \(\hat j\), \(\hat k\), which are the unit vectors along the x-axis, y-axis, and z-axis respectively. The vector equation of a line passing through a point with position vector \(\vec a\), and is parallel to a vector \(\vec b\) can be written as \(\overrightarrow r. \hat n\) = d. Similarly, we can also create the vector equation of a plane with unit normal vector \(\hat n\) is \(\vec r.\hat n\) = d

How To Find Vector Equation Of A Line?

The vector equation of a line can be found from any point on the vector having the position vector \(\vec a\), and a parallel vector \(\vec b\), and is \(\vec r = \vec a + λ\vec b\). Another form of vector equation of a line passing through two points with the position vector \(\vec a\), and \(\vec b\) is \(\vec r = \vec a + λ(\vec b - \vec a)\).

How To Find Vector Equation Of A Plane?

The vector equation of a plane having a unit normal vector \(\hat n\) and with a perpendicular distance of 'd' from the origin is \(\vec r. \hat n = d\). Further, there are three other methods of finding the vector equations, based on the input values available.

How To Solve Vector Equations?

The vector equations can be solved to a simplified form by changing it into a cartesian form. The vector equation of a line, (\vec r = \vec a + λ\vec b\) can be simplified and written in a cartesian form as \(\dfrac{x - x_1}{a} = \dfrac{y - y_1}{b} = \dfrac{z - z_1}{c}\).

Math worksheets and
visual curriculum