A day full of math games & activities. Find one near you.

Square Root of 675

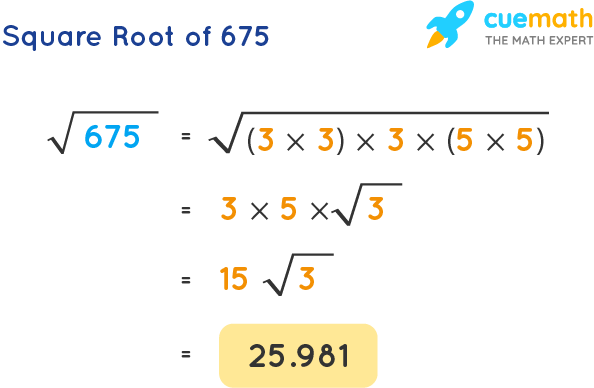
The square root of 675 is expressed as √675 in the radical form and as (675)^½ or (675)^0.5 in the exponent form. The square root of 675 rounded up to 9 decimal places is 25.980762114. It is the positive solution of the equation x² = 675. We can express the square root of 675 in its lowest radical form as 15 √3.

Square Root of 675: 25.98076211353316
Square Root of 675 in exponential form: (675)^½ or (675)^0.5
Square Root of 675 in radical form: √675 or 15 √3

Square Root of 675

1.	What is the Square Root of 675?
2.	How to find the Square Root of 675?
3.	Is the Square Root of 675 Irrational?
4.	FAQs

What is the Square Root of 675?

The square root of 675, (or root 675), is the number which when multiplied by itself gives the product as 675. Therefore, the square root of 675 = √675 = 15 √3 = 25.98076211353316.

☛ Check: Square Root Calculator

How to Find Square Root of 675?

Square Root of 675 by Long Division Method

Value of √675 by Long Division Method

Explanation:

Forming pairs: 06 and 75
Find a number Y (2) such that whose square is <= 6. Now divide 06 by 2 with quotient as 2.
Bring down the next pair 75, to the right of the remainder 2. The new dividend is now 275.
Add the last digit of the quotient (2) to the divisor (2) i.e. 2 + 2 = 4. To the right of 4, find a digit Z (which is 5) such that 4Z × Z <= 275. After finding Z, together 4 and Z (5) form a new divisor 45 for the new dividend 275.
Divide 275 by 45 with the quotient as 5, giving the remainder = 275 - 45 × 5 = 275 - 225 = 50.
Now, let's find the decimal places after the quotient 25.
Bring down 00 to the right of this remainder 50. The new dividend is now 5000.
Add the last digit of quotient to divisor i.e. 5 + 45 = 50. To the right of 50, find a digit Z (which is 9) such that 50Z × Z <= 5000. Together they form a new divisor (509) for the new dividend (5000).
Divide 5000 by 509 with the quotient as 9, giving the remainder = 5000 - 509 × 9 = 5000 - 4581 = 419.
Bring down 00 again. Repeat above steps for finding more decimal places for the square root of 675.

Therefore, the square root of 675 by long division method is 25.9 approximately.

Is Square Root of 675 Irrational?

The actual value of √675 is undetermined. The value of √675 up to 25 decimal places is 25.98076211353315940291170. Hence, the square root of 675 is an irrational number.

☛ Also Check:

Square Root of 56 - √56 = 7.48331
Square Root of 125 - √125 = 11.18034
Square Root of 625 - √625 = 25
Square Root of 324 - √324 = 18
Square Root of 784 - √784 = 28
Square Root of 42 - √42 = 6.48074
Square Root of 320 - √320 = 17.88854

Square Root of 675 Solved Examples

Example 1: Solve the equation x² − 675 = 0

Solution:

x² - 675 = 0 i.e. x² = 675
x = ±√675
Since the value of the square root of 675 is 25.981,
⇒ x = +√675 or -√675 = 25.981 or -25.981.
Example 2: If the area of a circle is 675π in². Find the radius of the circle.

Solution:

Let 'r' be the radius of the circle.
⇒ Area of the circle = πr² = 675π in²
⇒ r = ±√675 in
Since radius can't be negative,
⇒ r = √675
The square root of 675 is 25.981.
⇒ r = 25.981 in
Example 3: If the area of an equilateral triangle is 675√3 in². Find the length of one of the sides of the triangle.

Solution:

Let 'a' be the length of one of the sides of the equilateral triangle.
⇒ Area of the equilateral triangle = (√3/4)a² = 675√3 in²
⇒ a = ±√2700 in
Since length can't be negative,
⇒ a = √2700 = 2 √675
We know that the square root of 675 is 25.981.
⇒ a = 51.962 in

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on the Square Root of 675

What is the Value of the Square Root of 675?

The square root of 675 is 25.98076.

Why is the Square Root of 675 an Irrational Number?

Upon prime factorizing 675 i.e. 3³ × 5², 3 is in odd power. Therefore, the square root of 675 is irrational.

What is the Value of 11 square root 675?

The square root of 675 is 25.981. Therefore, 11 √675 = 11 × 25.981 = 285.788.

Evaluate 10 plus 17 square root 675

The given expression is 10 + 17 √675. We know that the square root of 675 is 25.981. Therefore, 10 + 17 √675 = 10 + 17 × 25.981 = 10 + 441.673 = 451.673

If the Square Root of 675 is 25.981. Find the Value of the Square Root of 6.75.

Let us represent √6.75 in p/q form i.e. √(675/100) = 6.75/10 = 2.598. Hence, the value of √6.75 = 2.598

What is the Square Root of -675?

The square root of -675 is an imaginary number. It can be written as √-675 = √-1 × √675 = i √675 = 25.98i
where i = √-1 and it is called the imaginary unit.

Math worksheets and
visual curriculum