A day full of math games & activities. Find one near you.

Square Root of 49

49 is a perfect square number which can be obtained by a square of 7 and it is also a composite number. Hence, the square root of 49 is a rational number. In this lesson, we will explore the concept of the square root of 49. This lesson also explains the square root of 49 in radical form along with solved examples.

Square Root of 49: √49 = 7
Square of 49: 49² = 2401

1.	What Is the Square Root of 49?
2.	Is Square Root of 49 Rational or Irrational?
3.	How to Find the Square Root of 49?
4.	Important Notes
5.	Challenging Questions
6.	FAQs on Square Root of 49

What Is the Square Root of 49?

The square root of 49 is obtained by the number whose square gives the original number.

√49 = 7

The answer obtained on squaring 7 is 49. Hence, 49 is a perfect square.

Is Square Root of 49 Rational or Irrational?

A rational number is a number that can be expressed in the form of p/q, where p and q are integers and q is not equal to 0. We already found that √49 = 7. 7 is a whole number and it can be expressed in p/q form easily. The number 7 is a rational number. So, the square root of 49 is a rational number.

How to Find the Square Root of 49?

We will discuss two methods of finding the square root of 49

Prime Factorization
Long division

Prime factorization is a way of expressing a number as a product of its prime factors.
The prime factorization of 49 is 49 = 7 × 7
To find the square root of 49, we take one number from each pair of the same numbers and we multiply them.
49 = 7 × 7
√49 = 7

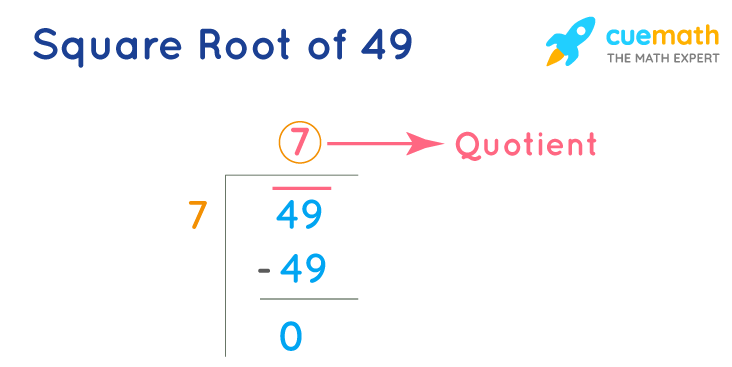
Square Root of 49 By Long Division

The value of the square root of 49 by long division method consists of the following steps:

Step 1: Starting from the right, we will pair up the digits by putting a bar above them.
Step 2: Find a number which, when multiplied to itself, gives the product less than or equal to 49. So, the number is 7. Putting the divisor as 7, we get the quotient as 7 and the remainder 0.
Step 3: The number 49 is a perfect square.

square root of 49 by long division

Explore square roots using illustrations and interactive examples

Important Notes:

The square root is the inverse operation of squaring.
49 is a perfect square as the answer obtained after square root is a rational number.
The square root of 49 can be simplified to 7 either by using the prime factorization of 49 or by expressing 49 as a square of 7.

Challenging Questions:

We know that (-7) × (-7) =49. So, can we say that -7 is a square root of 49?
Can you determine a quadratic equation whose roots are 49 and -49?

Example 1: Thomas says that the value of -(√49) is the same as (-√12). What do you think?

Solution

A negative square root cannot have real roots.
-(√49) has real roots but (-√49) has only imaginary roots.
Hence, they are not the same. -(√49) is not the same as (-√49).
Example 2: Help Ryan simplify the square root of 49 to its lowest radical form.

Solution

We need to express 49 as the product of its prime factors.
49 = 7 × 7
Therefore, √49 = 7
Thus, 7 is the lowest radical form.

go to slide go to slide

How can your child master math concepts?

Math mastery comes with practice and understanding the ‘Why’ behind the ‘What.’ Experience the Cuemath difference.

Book a Free Trial Class

go to slide go to slide go to slide

FAQs on Square Root of 49

What is the square root of 49?

The square root of 49 is 7.

What is the square of 7?

The square of 7 is 49.

How do you find the square root of 49?

We can find the square root of 49 by using the prime factorization and long division method.

Is the square root of 49 rational or irrational?

The square root of 49 is rational.

Is square root of 49 a real number?

Yes, the square root of 49 is a real number.

Math worksheets and
visual curriculum