A day full of math games & activities. Find one near you.

Square Root of 340

The square root of 340 is expressed as √340 in the radical form and as (340)^½ or (340)^0.5 in the exponent form. The square root of 340 rounded up to 9 decimal places is 18.439088915. It is the positive solution of the equation x² = 340. We can express the square root of 340 in its lowest radical form as 2 √85.

Square Root of 340: 18.439088914585774
Square Root of 340 in exponential form: (340)^½ or (340)^0.5
Square Root of 340 in radical form: √340 or 2 √85

Square Root of 340

1.	What is the Square Root of 340?
2.	How to find the Square Root of 340?
3.	Is the Square Root of 340 Irrational?
4.	FAQs

What is the Square Root of 340?

The square root of 340, (or root 340), is the number which when multiplied by itself gives the product as 340. Therefore, the square root of 340 = √340 = 2 √85 = 18.439088914585774.

☛ Check: Square Root Calculator

How to Find Square Root of 340?

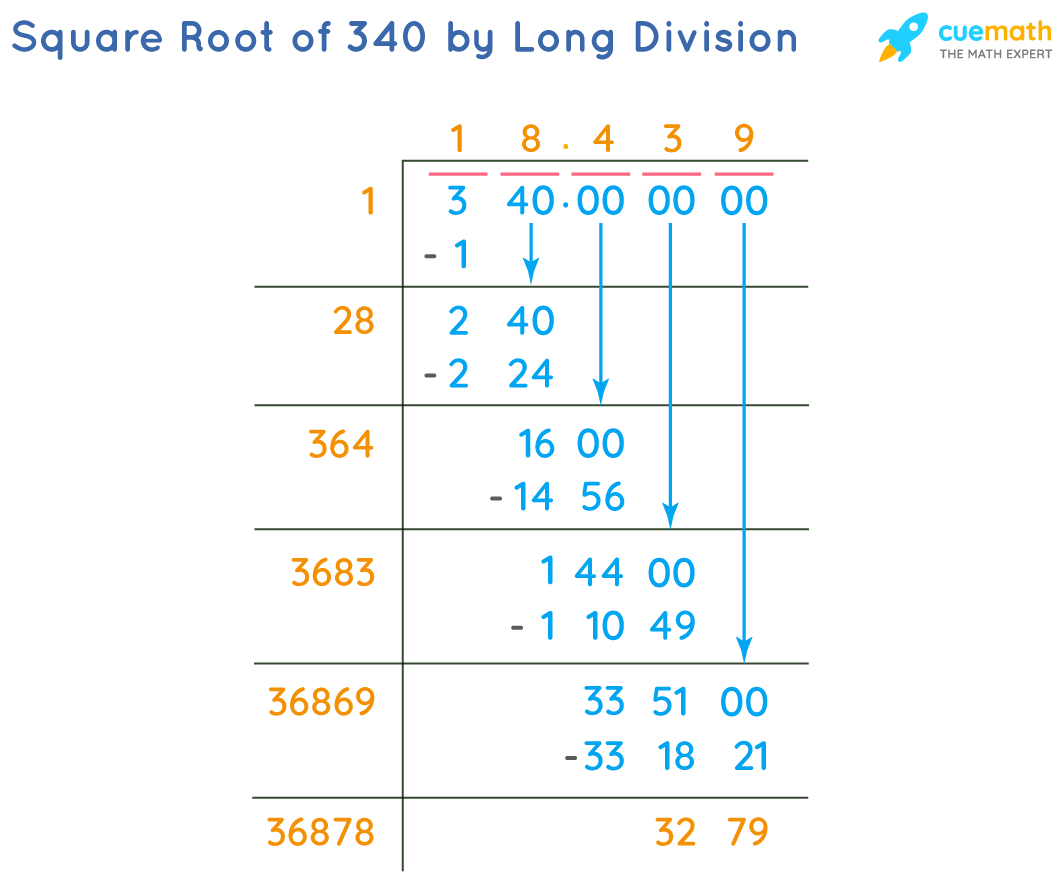
Square Root of 340 by Long Division Method

Value of √340 by Long Division Method

Explanation:

Forming pairs: 03 and 40
Find a number Y (1) such that whose square is <= 3. Now divide 03 by 1 with quotient as 1.
Bring down the next pair 40, to the right of the remainder 2. The new dividend is now 240.
Add the last digit of the quotient (1) to the divisor (1) i.e. 1 + 1 = 2. To the right of 2, find a digit Z (which is 8) such that 2Z × Z <= 240. After finding Z, together 2 and Z (8) form a new divisor 28 for the new dividend 240.
Divide 240 by 28 with the quotient as 8, giving the remainder = 240 - 28 × 8 = 240 - 224 = 16.
Now, let's find the decimal places after the quotient 18.
Bring down 00 to the right of this remainder 16. The new dividend is now 1600.
Add the last digit of quotient to divisor i.e. 8 + 28 = 36. To the right of 36, find a digit Z (which is 4) such that 36Z × Z <= 1600. Together they form a new divisor (364) for the new dividend (1600).
Divide 1600 by 364 with the quotient as 4, giving the remainder = 1600 - 364 × 4 = 1600 - 1456 = 144.
Bring down 00 again. Repeat above steps for finding more decimal places for the square root of 340.

Therefore, the square root of 340 by long division method is 18.4 approximately.

Is Square Root of 340 Irrational?

The actual value of √340 is undetermined. The value of √340 up to 25 decimal places is 18.43908891458577462000455. Hence, the square root of 340 is an irrational number.

☛ Also Check:

Square Root of 100 - √100 = 10
Square Root of 361 - √361 = 19
Square Root of 162 - √162 = 12.72792
Square Root of 320 - √320 = 17.88854
Square Root of 99 - √99 = 9.94987
Square Root of 90 - √90 = 9.48683
Square Root of 51 - √51 = 7.14143

Square Root of 340 Solved Examples

Example 1: Solve the equation x² − 340 = 0

Solution:

x² - 340 = 0 i.e. x² = 340
x = ±√340
Since the value of the square root of 340 is 18.439,
⇒ x = +√340 or -√340 = 18.439 or -18.439.
Example 2: If the area of a circle is 340π in². Find the radius of the circle.

Solution:

Let 'r' be the radius of the circle.
⇒ Area of the circle = πr² = 340π in²
⇒ r = ±√340 in
Since radius can't be negative,
⇒ r = √340
The square root of 340 is 18.439.
⇒ r = 18.439 in
Example 3: If the surface area of a cube is 2040 in². Find the length of the side of the cube.

Solution:

Let 'a' be the length of the side of the cube.
⇒ Area of the cube = 6a² = 2040 in²
⇒ a = ±√340 in
Since length can't be negative,
⇒ a = √340
We know that the square root of 340 is 18.439.
⇒ a = 18.439 in

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on the Square Root of 340

What is the Value of the Square Root of 340?

The square root of 340 is 18.43908.

Why is the Square Root of 340 an Irrational Number?

Upon prime factorizing 340 i.e. 2² × 5¹ × 17¹, 5 is in odd power. Therefore, the square root of 340 is irrational.

What is the Value of 15 square root 340?

The square root of 340 is 18.439. Therefore, 15 √340 = 15 × 18.439 = 276.586.

If the Square Root of 340 is 18.439. Find the Value of the Square Root of 3.4.

Let us represent √3.4 in p/q form i.e. √(340/100) = 3.4/10 = 1.844. Hence, the value of √3.4 = 1.844

What is the Square of the Square Root of 340?

The square of the square root of 340 is the number 340 itself i.e. (√340)² = (340)^2/2 = 340.

What is the Square Root of 340 in Simplest Radical Form?

We need to express 340 as the product of its prime factors i.e. 340 = 2 × 2 × 5 × 17. Therefore, √340 = √2 × 2 × 5 × 17 = 2 √85. Thus, the square root of 340 in the lowest radical form is 2 √85.

Math worksheets and
visual curriculum