Linear Programming
Linear programming is a process that is used to determine the best outcome of a linear function. It is the best method to perform linear optimization by making a few simple assumptions. The linear function is known as the objective function. Real-world relationships can be extremely complicated. However, linear programming can be used to depict such relationships, thus, making it easier to analyze them.
Linear programming is used in many industries such as energy, telecommunication, transportation, and manufacturing. This article sheds light on the various aspects of linear programming such as the definition, formula, methods to solve problems using this technique, and associated linear programming examples.
What is Linear Programming?
Linear programming, also abbreviated as LP, is a simple method that is used to depict complicated real-world relationships by using a linear function. The elements in the mathematical model so obtained have a linear relationship with each other. Linear programming is used to perform linear optimization so as to achieve the best outcome.
Linear Programming Definition
Linear programming can be defined as a technique that is used for optimizing a linear function in order to reach the best outcome. This linear function or objective function consists of linear equality and inequality constraints. We obtain the best outcome by minimizing or maximizing the objective function.
Linear Programming Examples
Suppose a postman has to deliver 6 letters in a day from the post office (located at A) to different houses (U, V, W, Y, Z). The distance between the houses is indicated on the lines as given in the image. If the postman wants to find the shortest route that will enable him to deliver the letters as well as save on fuel then it becomes a linear programming problem. Thus, LP will be used to get the optimal solution which will be the shortest route in this example.

Linear Programming Formula
A linear programming problem will consist of decision variables, an objective function, constraints, and non-negative restrictions. The decision variables, x, and y, decide the output of the LP problem and represent the final solution. The objective function, Z, is the linear function that needs to be optimized (maximized or minimized) to get the solution. The constraints are the restrictions that are imposed on the decision variables to limit their value. The decision variables must always have a non-negative value which is given by the non-negative restrictions. The general formula of a linear programming problem is given below:
Objective Function: Z = ax + by
Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
Non-negative restrictions: x ≥ 0, y ≥ 0
How to Solve Linear Programming Problems?
The most important part of solving linear programming problem is to first formulate the problem using the given data. The steps to solve linear programming problems are given below:
- Step 1: Identify the decision variables.
- Step 2: Formulate the objective function. Check whether the function needs to be minimized or maximized.
- Step 3: Write down the constraints.
- Step 4: Ensure that the decision variables are greater than or equal to 0. (Non-negative restraint)
- Step 5: Solve the linear programming problem using either the simplex or graphical method.
Let us study about these methods in detail in the following sections.
Linear Programming Methods
There are two main methods available for solving linear programming problem. These are the simplex method and the graphical method. Given below are the steps to solve a linear programming problem using both methods.
Linear Programming by Simplex Method
The simplex method in lpp can be applied to problems with two or more decision variables. Suppose the objective function Z = 40\(x_{1}\) + 30\(x_{2}\) needs to be maximized and the constraints are given as follows:
\(x_{1}\) + \(x_{2}\) ≤ 12
2\(x_{1}\) + \(x_{2}\) ≤ 16
\(x_{1}\) ≥ 0, \(x_{2}\) ≥ 0
Step 1: Add another variable, known as the slack variable, to convert the inequalities into equations. Also, rewrite the objective function as an equation.
- 40\(x_{1}\) - 30\(x_{2}\) + Z = 0
\(x_{1}\) + \(x_{2}\) + \(y_{1}\) =12
2\(x_{1}\) + \(x_{2}\) + \(y_{2}\) =16
\(y_{1}\) and \(y_{2}\) are the slack variables.
Step 2: Construct the initial simplex matrix as follows:
\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 2& 1 & 0& 1 & 0 & 16 \\ -40&-30&0&0&1&0 \end{bmatrix}\)
Step 3: Identify the column with the highest negative entry. This is called the pivot column. As -40 is the highest negative entry, thus, column 1 will be the pivot column.
Step 4: Divide the entries in the rightmost column by the entries in the pivot column. We exclude the entries in the bottom-most row.
12 / 1 = 12
16 / 2 = 8
The row containing the smallest quotient is identified to get the pivot row. As 8 is the smaller quotient as compared to 12 thus, row 2 becomes the pivot row. The intersection of the pivot row and the pivot column gives the pivot element.
Thus, pivot element = 2.
Step 5: With the help of the pivot element perform pivoting, using matrix properties, to make all other entries in the pivot column 0.
Using the elementary operations divide row 2 by 2 (\(R_{2}\) / 2)
\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)
Now apply \(R_{1}\) = \(R_{1}\) - \(R_{2}\)
\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)
Finally \(R_{3}\) = \(R_{3}\) + 40\(R_{2}\) to get the required matrix.
\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ 0&-10&0&20&1&320 \end{bmatrix}\)
Step 6: Check if the bottom-most row has negative entries. If no, then the optimal solution has been determined. If yes, then go back to step 3 and repeat the process. -10 is a negative entry in the matrix thus, the process needs to be repeated. We get the following matrix.
\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1 &2 &-1 &0 &8 \\ 1& 0 & -1& 1 & 0 & 4 \\ 0&0&20&10&1&400 \end{bmatrix}\)
Writing the bottom row in the form of an equation we get Z = 400 - 20\(y_{1}\) - 10\(y_{2}\). Thus, 400 is the highest value that Z can achieve when both \(y_{1}\) and \(y_{2}\) are 0.
Also, when \(x_{1}\) = 4 and \(x_{2}\) = 8 then value of Z = 400
Thus, \(x_{1}\) = 4 and \(x_{2}\) = 8 are the optimal points and the solution to our linear programming problem.
Linear Programming by Graphical Method
If there are two decision variables in a linear programming problem then the graphical method can be used to solve such a problem easily.
Suppose we have to maximize Z = 2x + 5y.
The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9
where, x ≥ 0 and y ≥ 0.
To solve this problem using the graphical method the steps are as follows.
Step 1: Write all inequality constraints in the form of equations.
x + 4y = 24
3x + y = 21
x + y = 9
Step 2: Plot these lines on a graph by identifying test points.
x + 4y = 24 is a line passing through (0, 6) and (24, 0). [By substituting x = 0 the point (0, 6) is obtained. Similarly, when y = 0 the point (24, 0) is determined.]
3x + y = 21 passes through (0, 21) and (7, 0).
x + y = 9 passes through (9, 0) and (0, 9).
Step 3: Identify the feasible region. The feasible region can be defined as the area that is bounded by a set of coordinates that can satisfy some particular system of inequalities.
Any point that lies on or below the line x + 4y = 24 will satisfy the constraint x + 4y ≤ 24.
Similarly, a point that lies on or below 3x + y = 21 satisfies 3x + y ≤ 21.
Also, a point lying on or below the line x + y = 9 satisfies x + y ≤ 9.
The feasible region is represented by OABCD as it satisfies all the above-mentioned three restrictions.
Step 4: Determine the coordinates of the corner points. The corner points are the vertices of the feasible region.
O = (0, 0)
A = (7, 0)
B = (6, 3). B is the intersection of the two lines 3x + y = 21 and x + y = 9. Thus, by substituting y = 9 - x in 3x + y = 21 we can determine the point of intersection.
C = (4, 5) formed by the intersection of x + 4y = 24 and x + y = 9
D = (0, 6)
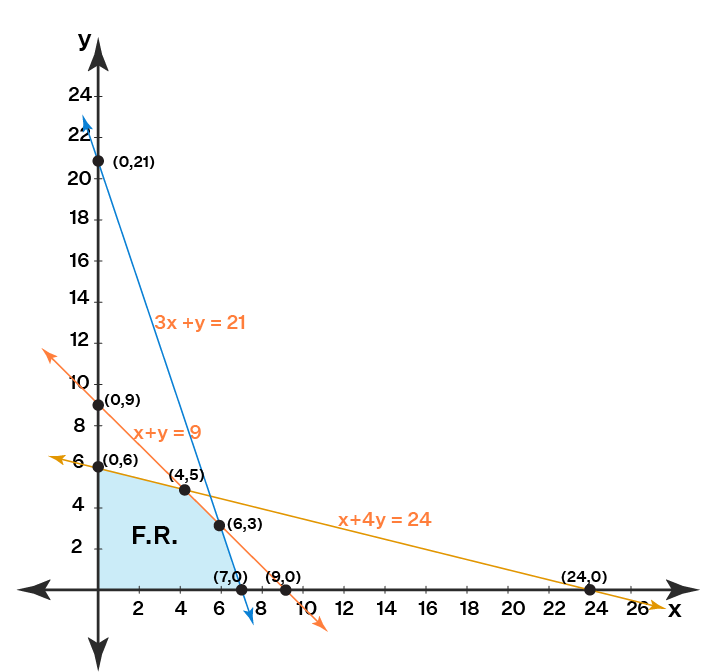
Step 5: Substitute each corner point in the objective function. The point that gives the greatest (maximizing) or smallest (minimizing) value of the objective function will be the optimal point.
| Corner Points | Z = 2x + 5y |
| O = (0, 0) | 0 |
| A = (7, 0) | 14 |
| B = (6, 3) | 27 |
| C = (4, 5) | 33 |
| D = (0, 6) | 30 |
33 is the maximum value of Z and it occurs at C. Thus, the solution is x = 4 and y = 5.
Applications of Linear Programming
Linear programming is used in several real-world applications. It is used as the basis for creating mathematical models to denote real-world relationships. Some applications of LP are listed below:
- Manufacturing companies make widespread use of linear programming to plan and schedule production.
- Delivery services use linear programming to decide the shortest route in order to minimize time and fuel consumption.
- Financial institutions use linear programming to determine the portfolio of financial products that can be offered to clients.
Related Articles:
- Lines
- Introduction to Graphing
- Linear Equations in Two Variables
- Solutions of a Linear Equation
- Mathematical Induction
Important Notes on Linear Programming
- Linear programming is a technique that is used to determine the optimal solution of a linear objective function.
- The simplex method in lpp and the graphical method can be used to solve a linear programming problem.
- In a linear programming problem, the variables will always be greater than or equal to 0.
Linear Programming Examples
-
Example 1: Solve the following linear programming problem using the graphical method.
Minimize: Z = 5x + 4y
4x + y ≥ 40,
2x + 3y ≥ 90,
x, y ≥ 0
Solution: Using the constraints we get the equations of the lines as 4x + y = 40 and 2x + 3y = 90.
4x + y = 40 passes through (0, 40) and (10, 0). Any point lying on or above this line satisfies 4x + y ≥ 40
2x + 3y = 90 passes through (0, 30) and (45, 0). Any point lying on or above this line satisfies 2x + 3y ≥ 90. The graph is given as

Corner Points Z = 5x + 4y A = (45, 0) 225 B = (3, 28) 127 C = (0, 40) 160 As the minimum value of Z is 127, thus, B (3, 28) gives the optimal solution.
Answer: The minimum value of Z is 127 and the optimal solution is (3, 28) -
Example 2: Solve the linear programming problem using the graphical method.
Maximize Z = 2x + 3y
x + y ≤ 30,
x ≤ 20, y ≤ 12
x, y ≥ 0
Solution: Writing the inequalities as equations we get,
x + y = 30 passing through (0, 30) and (30, 0). Points on or below this line will satisfy x + y ≤ 30
x = 20 is a line parallel to the y axis. Any point on or to the left of this line will satisfy x ≤ 20.
y = 12 is a line parallel to the x axis. Any point on or below this line will satisfy y ≤ 12. The graph is given by

The maximum value of Z = 72 and it occurs at C (18, 12)Corner points Z = 2x + 3y O = (0, 0) 0 A = (20, 0) 40 B = (20, 10) 70 C = (18, 12) 72 D = (0, 12) 36
Answer: the maximum value of Z = 72 and the optimal solution is (18, 12) -
Example 3: Using the simplex method in lpp solve the linear programming problem
Minimize Z = \(x_{1}\) + 2\(x_{2}\) + 3\(x_{3}\)
\(x_{1}\) + \(x_{2}\) + \(x_{3}\) ≤ 12
2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) ≤ 18
\(x_{1}\), \(x_{2}\), \(x_{3}\) ≥ 0
Solution: Convert all inequalities to equations by introducing slack variables.
-\(x_{1}\) - 2\(x_{2}\) - 3\(x_{3}\) + Z = 0
\(x_{1}\) + \(x_{2}\) + \(x_{3}\) + \(y_{1}\) = 12
2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) + \(y_{2}\) = 18
Expressing this as a matrix we get,
\(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 1 & 1 & 1 & 1 & 0 & 0 & 12\\ 2 & 1 & 3 & 0 & 1 & 0 & 18\\ -1 & -2 & -3 & 0 & 0 & 1 & 0 \end{bmatrix}\)
As -3 is the greatest negative value thus, column 3 is the pivot column.
12 / 1 = 12
18 / 3 = 6
As 6 is the smaller quotient thus, row 2 is the pivot row and 3 is the pivot element. By applying matrix operations we get,
\(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.33 & 0.667 & 0 & 1 & -0.33 & 0 & 6\\ 0.667 & 0.33 & 1 & 0 & 0.33 & 0 & 6\\ 1 & -1 & 0 & 0 & 1 & 1 & 18 \end{bmatrix}\)
Now -1 needs to be eliminated. Thus, by repreating the steps the matrix so obtained is as follows
\(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.5 & 1 & 0 & 1.5 & 0.5 & 0 & 9\\ 0.5 & 0 & 1 & -0.5 & 0.5 & 0 & 3\\ 1.5 & 0 & 0 & 1.5 & 0.5 & 1 & 27 \end{bmatrix}\)
We get the maximum value of Z = 27 at \(x_{1}\) = 0, \(x_{2}\) = 9 \(x_{3}\) = 3
Answer: Maximum value of Z = 27 and optimal solution (0, 9, 3)

FAQs on Linear Programming
What is Meant by Linear Programming?
Linear programming is a technique that is used to identify the optimal solution of a function wherein the elements have a linear relationship.
What is Linear Programming Formula?
The general formula for a linear programming problem is given as follows:
- Objective Function: Z = ax + by
- Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
- Non-negative restrictions: x ≥ 0, y ≥ 0
What is the Objective Function in Linear Programming Problems?
The objective function is the linear function that needs to be maximized or minimized and is subject to certain constraints. It is of the form Z = ax + by.
How to Formulate a Linear Programming Model?
The steps to formulate a linear programming model are given as follows:
- Identify the decision variables.
- Formulate the objective function.
- Identify the constraints.
- Solve the obtained model using the simplex or the graphical method.
How to Find Optimal Solution in Linear Programming?
We can find the optimal solution in a linear programming problem by using either the simplex method or the graphical method. The simplex method in lpp can be applied to problems with two or more variables while the graphical method can be applied to problems containing 2 variables only.
How to Find Feasible Region in Linear Programming?
To find the feasible region in a linear programming problem the steps are as follows:
- Draw the straight lines of the linear inequalities of the constraints.
- Use the "≤" and "≥" signs to denote the feasible region of each constraint.
- The region common to all constraints will be the feasible region for the linear programming problem.
What are Linear Programming Uses?
Linear programming is widely used in many industries such as delivery services, transportation industries, manufacturing companies, and financial institutions. The linear program is solved through linear optimization method, and it is used to determine the best outcome in a given scenerio.
visual curriculum
