

(a - b - c)^2 Formula
The (a - b - c)2 formula is used to find the square of the difference between the three numbers without actually calculating the whole square and in factorization. (a - b - c)2 formula is one of the major algebraic identities. To derive the expansion of (a - b - c)2 formula we just multiply (a - b - c) by itself to get (a - b - c)2. Let us learn more about the (a - b - c)2 formula along with solved examples.
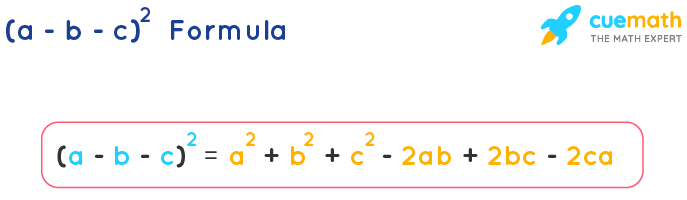
What Is (a - b - c)2 Formula?
We just read that by multiplying (a - b - c) by itself we can easily derive the (a - b - c)2 formula. Let us see the expansion of (a - b - c)2 formula.
(a - b - c)2 = (a - b - c)(a - b - c)
(a - b - c)2 = a2 - ab - ac - ab + b2 + bc - ca + bc + c2
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca
(a - b - c)2 = a2 + b2 + c2 - 2(ab - bc + ca)
Let us see how to use the (a - b - c)2 formula in the following section.

Examples on (a - b - c)2 Formula
Let us take a look at a few examples to better understand the formula of (a - b - c)2.
Example 1: Find the value of (a - b - c)2 if a = 2, b = 4, and c = 3 using (a - b - c)2 formula.
Solution:
To find: (a - b - c)2
Given that:
a = 2, b = 4, c = 3
Using the (a - b - c)2 formula,
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca
(a - b - c)2 = 22 + 42 + 32 - 2(2)(4) +2(4)(3) - 2(3)(2)
(a - b - c)2 = 4 + 16 + 9 - 16 + 24 - 12
Answer: (a - b - c)2 = 25.
Example 2: Find the value of (a - b - c)2 if a = 12, b = 4, and c = 5 using (a - b - c)2 formula.
Solution:
To find: (a - b - c)2
Given that:
a = 12, b = 4, c = 5
Using the (a - b - c)2 formula,
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca
(a - b - c)2 = 122 + 42 + 52 - 2(12)(4) +2(4)(5) - 2(5)(12)
(a - b - c)2 = 144 + 16 + 25 - 96 + 40 - 120 = 9
Answer: (a - b - c)2 = 9.
Example 3: Find the value of a2 + b2 + c2 if (ab - bc + ca) = 10 and (a - b - c) = 20 using (a - b - c)2 formula.
Solution:
To find: a2 + b2 + c2
Given that:
(ab-bc+ca) = 10 and (a - b - c) = 20
Using the (a - b - c)2 formula,
(a - b - c)2 = a2 + b2 + c2 - 2(ab - bc + ca)
(20)2 = a2 + b2 + c2 - 2(10)
400 = a2 + b2 + c2 - 20
a2 + b2 + c2 = 400 + 20 = 420
Answer: (a - b - c)2 = 420.
FAQs on (a - b - c)2 Formulas
What Is the Expansion of (a - b - c)2 Formula?
(a - b - c)2 formula is read as a minus b minus c whole square. Its expansion is expressed as (a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca.
What Is the a2 - b2 - c2 Formula in Algebra?
The (a - b - c)2 formula is one of the important algebraic identities. It is read as a minus b minus c whole square. The (a - b - c)2 formula is expressed as (a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca.
How To Simplify Numbers Using the (a - b - c)2 Formula?
Let us understand the use of the (a - b - c)2 formula with the help of the following example.
Example: Find the value of (2 - 5 - 3)2 using the (a - b - c)2 formula.
To find: (2 - 5 - 3)2
Let us assume that a = 2 and b = 5 and c = 3.
We will substitute these in the formula of (a - b - c)2.
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca
= 22 + 52 + 32 - 2(2*5) + 2(5*3) - 2(3*2)
= 4 + 25 + 9 - 2(10) + 2(15) - 2(6)
Answer: (2 - 5 - 3)2 = 36
How To Use the (a - b - c)2 Formula Give Steps?
The following steps are followed while using (a - b - c)2 formula.
- Firstly observe the pattern of the numbers whether the three numbers have ^2 as whole power or not such as (a - b - c)2.
- Write down the formula of (a - b - c)2.
- (a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca.
- substitute the value of a, b and c in the (a - b - c)2 formula and simplify.
visual curriculum