A day full of math games & activities. Find one near you.

GCF of 8 and 11

GCF of 8 and 11 is the largest possible number that divides 8 and 11 exactly without any remainder. The factors of 8 and 11 are 1, 2, 4, 8 and 1, 11 respectively. There are 3 commonly used methods to find the GCF of 8 and 11 - prime factorization, long division, and Euclidean algorithm.

1.	GCF of 8 and 11
2.	List of Methods
3.	Solved Examples
4.	FAQs

What is GCF of 8 and 11?

Answer: GCF of 8 and 11 is 1.

Explanation:

The GCF of two non-zero integers, x(8) and y(11), is the greatest positive integer m(1) that divides both x(8) and y(11) without any remainder.

Methods to Find GCF of 8 and 11

The methods to find the GCF of 8 and 11 are explained below.

Using Euclid's Algorithm
Prime Factorization Method
Long Division Method

GCF of 8 and 11 by Euclidean Algorithm

As per the Euclidean Algorithm, GCF(X, Y) = GCF(Y, X mod Y)
where X > Y and mod is the modulo operator.

Here X = 11 and Y = 8

GCF(11, 8) = GCF(8, 11 mod 8) = GCF(8, 3)
GCF(8, 3) = GCF(3, 8 mod 3) = GCF(3, 2)
GCF(3, 2) = GCF(2, 3 mod 2) = GCF(2, 1)
GCF(2, 1) = 1 (∵ GCF(X, 1) = 1)

Therefore, the value of GCF of 8 and 11 is 1.

GCF of 8 and 11 by Prime Factorization

Prime factorization of 8 and 11 is (2 × 2 × 2) and (11) respectively. As visible, there are no common prime factors between 8 and 11, i.e. they are coprime. Hence, the GCF of 8 and 11 will be 1.

GCF of 8 and 11 by Long Division

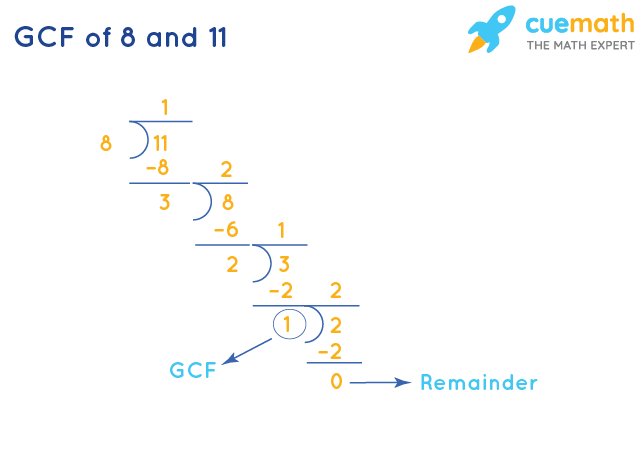
GCF of 8 and 11 is the divisor that we get when the remainder becomes 0 after doing long division repeatedly.

Step 1: Divide 11 (larger number) by 8 (smaller number).
Step 2: Since the remainder ≠ 0, we will divide the divisor of step 1 (8) by the remainder (3).
Step 3: Repeat this process until the remainder = 0.

The corresponding divisor (1) is the GCF of 8 and 11.

☛ Also Check:

GCF of 8 and 11 Examples

Example 1: For two numbers, GCF = 1 and LCM = 88. If one number is 11, find the other number.

Solution:

Given: GCF (y, 11) = 1 and LCM (y, 11) = 88
∵ GCF × LCM = 11 × (y)
⇒ y = (GCF × LCM)/11
⇒ y = (1 × 88)/11
⇒ y = 8
Therefore, the other number is 8.
Example 2: Find the GCF of 8 and 11, if their LCM is 88.

Solution:

∵ LCM × GCF = 8 × 11
⇒ GCF(8, 11) = (8 × 11)/88 = 1
Therefore, the greatest common factor of 8 and 11 is 1.
Example 3: Find the greatest number that divides 8 and 11 exactly.

Solution:

The greatest number that divides 8 and 11 exactly is their greatest common factor, i.e. GCF of 8 and 11.
⇒ Factors of 8 and 11:
- Factors of 8 = 1, 2, 4, 8
- Factors of 11 = 1, 11
Therefore, the GCF of 8 and 11 is 1.

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on GCF of 8 and 11

What is the GCF of 8 and 11?

The GCF of 8 and 11 is 1. To calculate the GCF (Greatest Common Factor) of 8 and 11, we need to factor each number (factors of 8 = 1, 2, 4, 8; factors of 11 = 1, 11) and choose the greatest factor that exactly divides both 8 and 11, i.e., 1.

What is the Relation Between LCM and GCF of 8, 11?

The following equation can be used to express the relation between LCM and GCF of 8 and 11, i.e. GCF × LCM = 8 × 11.

What are the Methods to Find GCF of 8 and 11?

There are three commonly used methods to find the GCF of 8 and 11.

By Listing Common Factors
By Long Division
By Prime Factorization

How to Find the GCF of 8 and 11 by Long Division Method?

To find the GCF of 8, 11 using long division method, 11 is divided by 8. The corresponding divisor (1) when remainder equals 0 is taken as GCF.

How to Find the GCF of 8 and 11 by Prime Factorization?

To find the GCF of 8 and 11, we will find the prime factorization of the given numbers, i.e. 8 = 2 × 2 × 2; 11 = 11.
⇒ There is no common prime factor for 8 and 11. Hence, GCF (8, 11) = 1.
☛ What are Prime Numbers?

If the GCF of 11 and 8 is 1, Find its LCM.

GCF(11, 8) × LCM(11, 8) = 11 × 8
Since the GCF of 11 and 8 = 1
⇒ 1 × LCM(11, 8) = 88
Therefore, LCM = 88
☛ Greatest Common Factor Calculator

Download FREE Study Materials

GCF and LCM

Math worksheets and
visual curriculum