Cubic Function
A cubic function is a polynomial function of degree 3. So the graph of a cube function may have a maximum of 3 roots. i.e., it may intersect the x-axis at a maximum of 3 points. Since complex roots always occur in pairs, a cubic function always has either 1 or 3 real zeros. It cannot have 2 real zeros.
Let us learn more about a cubic function along with its domain, range, and the process of graphing it. Let us also learn how to find the critical points and inflection points of a cube function and let us also see its end behavior.
| 1. | What is Cubic Function? |
| 2. | Intercepts of a Cubic Function |
| 3. | End Behavior of Cube Function |
| 4. | Critical and Inflection Points of Cubic Function |
| 5. | Cubic Graph |
| 6. | FAQs on Cubic Function |
What is Cubic Function?
A cubic function is a polynomial function of degree 3 and is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, and d are real numbers and a ≠ 0. The basic cubic function (which is also known as the parent cube function) is f(x) = x3. Since a cubic function involves an odd degree polynomial, it has at least one real root. For example, there is only one real number that satisfies x3 = 0 (which is x = 0) and hence the cubic function f(x) = x3 has only one real root (the other two roots are complex numbers). Here are some examples of a cubic function.

A cubic function is an algebraic function as all algebraic functions are polynomial functions.
Domain and Range of Cubic Function
Since a cubic function y = f(x) is a polynomial function, it is defined for all real values of x and hence its domain is the set of all real numbers (R). Also, if you observe the two examples (in the above figure), all y-values are being covered by the graph, and hence the range of a cubic function is the set of all numbers as well. Thus, we conclude that
- The domain of a cubic function is R.
- The range of a cubic function is R.
Asymptotes of Cube Function
The asymptotes always correspond to the values that are excluded from the domain and range. Since both the domain and range of a cubic function is the set of all real numbers, no values are excluded from either the domain or the range. Hence a cubic function neither has vertical asymptotes nor has horizontal asymptotes.
Intercepts of a Cubic Function
As we know, there are two types of intercepts of a function: x-intercept(s) and y-intercept(s). Let us see how to find the intercepts of a cubic function.
X-Intercept of Cubic Function
The x-intercepts of a function are also known as roots (or) zeros. As the degree of a cubic function is 3, it can have a maximum of 3 roots. Since complex roots of any function always occur in pairs, a function will always have 0, 2, 4, ... complex roots. So a function can either have 0 or two complex roots. Thus, it has one or three real roots or x-intercepts. To find the x-intercept(s) of a cubic function, we just substitute y = 0 (or f(x) = 0) and solve for x-values.
Example: To find the x-intercept(s) of f(x) = x3 - 4x2 + x - 4, substitute f(x) = 0. Then
x3 - 4x2 + x - 4 = 0
x2 (x - 4) + 1 (x - 4) = 0
(x - 4) (x2 + 1) = 0
x - 4 = 0; x2 + 1 = 0
x = 4 ; x2 = -1
x = 4 ; x = ± i
Complex numbers cannot be the x-intercepts. Therefore, f(x) has only one x-intercept which is (4, 0).
Y-Intercept of Cubic Function
A cubic function always has exactly one y-intercept. To find the y-intercept of a cubic function, we just substitute x = 0 and solve for y-value.
Example: To find the y-intercept of f(x) = x3 - 4x2 + x - 4, substitute x = 0. Then f(x) = 03 - 4(0)2 + (0) - 4 = -4.
Therefore, the y-intercept of the function is (0, -4).
End Behavior of Cube Function
The end behavior of any function depends upon its degree and the sign of the leading coefficient. A cube function f(x) = ax3 + bx2 + cx + d has an odd degree polynomial in it. So its end behavior is as follows:
- When the leading coefficient is positive (a > 0):
f(x) → ∞ as x → ∞ and
f(x) → -∞ as x → -∞
In this case, the shape of the graph is from bottom to top. - When the leading coefficient is negative (a < 0):
f(x) → -∞ as x → ∞ and
f(x) → ∞ as x → -∞
In this case, the shape of the graph is from top to bottom.
We can better understand this from the figure below:

Critical and Inflection Points of Cubic Function
The critical points and inflection points play a crucial role in graphing a cubic function. Let us see how to find them.
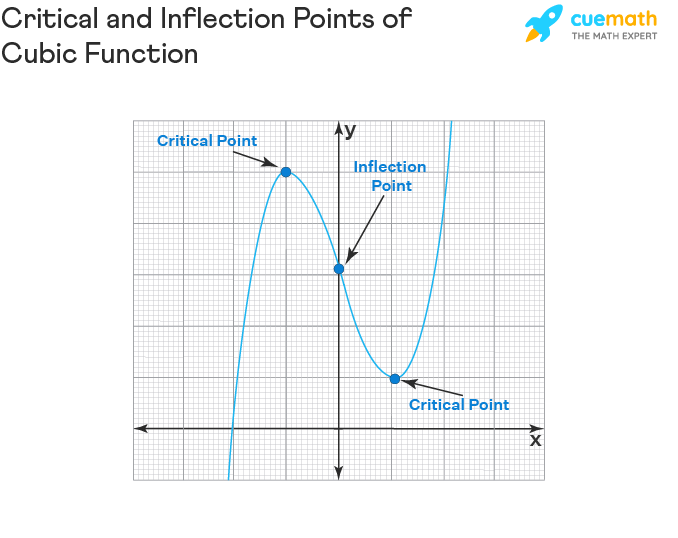
Critical Points of Cubic Function
The critical points of a function are the points where the function changes from either "increasing to decreasing" or "decreasing to increasing". i.e., a function may have either a maximum or minimum value at the critical point. To find the critical points of a cubic function f(x) = ax3 + bx2 + cx + d, we set the first derivative to zero and solve. i.e.,
f'(x) = 0
3ax2 + 2bx + c = 0
This is a quadratic equation and we can solve it using the techniques of solving quadratic equations.
x = \(\dfrac{-2b \pm \sqrt{4b^{2}-12 a c}}{6 a}\) (or)
x = \(\dfrac{-b \pm \sqrt{b^{2}-3 a c}}{3 a}\)
Hence:
- f(x) has two critical points if b2 - 3ac > 0
- f(x) has only one critical point if b2 - 3ac = 0
- f(x) has no critical point if b2 - 3ac < 0
Inflection Points of Cubic Function
The inflection points of a function are the points where the function changes from either "concave up to concave down" or "concave down to concave up". To find the critical points of a cubic function f(x) = ax3 + bx2 + cx + d, we set the second derivative to zero and solve. i.e.,
f''(x) = 0
6ax + 2b = 0
6ax = -2b
x = -b/3a
Thus, the cubic function f(x) = ax3 + bx2 + cx + d has inflection point at (-b/3a, f(-b/3a)).
Cubic Graph
Here are the steps to graph a cubic function. The steps are explained with an example where we are going to graph the cubic function f(x) = x3 - 4x2 + x - 4.
- Step 1: Find the x-intercept(s).
We already found that the x-intercept of f(x) = x3 - 4x2 + x - 4 is (4, 0). - Step 2: Find the y-intercept.
We already found that the y-intercept of f(x) = x3 - 4x2 + x - 4 is (0, -4). - Step 3: Find the critical point(s) by setting f'(x) = 0.
3x2 - 8x + 1 = 0.
By quadratic formula,
x = (-8 ± √64 - 12) / (6) ≈ 0.131 and 2.535 - Step 4: Find the corresponding y-coordinate(s) of the critical points by substituting each of them in the given function.
f(0.131) ≈ -3.935
f(2.535) ≈ -10.879
Therefore, the critical points are (0.131, -3.935) and (2.535, -10.879). - Step 5: Find the end behavior of the function.
Since the leading coefficient of the function is 1 which is > 0, its end behavior is:
f(x) → ∞ as x → ∞ and
f(x) → -∞ as x → -∞ - Step 6: Plot all the points from Step 1, Step 2, and Step 4. Join them by a curve (also extend the curve on both sides) keeping the end behavior from Step 5 in mind.

Note: We can compute a table of values by taking some random numbers for x and computing the corresponding y values to know the perfect shape of the graph. Also, we can find the inflection point and cross-check the graph.
Important Notes on Cubic Function:
- A cubic function is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, and d are constants and a ≠ 0.
- The degree of a cubic function is 3.
- A cubic function may have 1 or 3 real roots.
- A cubic function may have 0 or 2 complex roots.
- A cubic function is maximum or minimum at the critical points.
☛Related Topics:
Examples on Cubic Function
-
Example 1: Find the x intercept(s) and y intercept of cubic function: f(x) = 3 (x - 1) (x - 2) (x - 3).
Solution:
X-intercept(s): To find the x-intercepts, substitute f(x) = 0.
Then 3 (x - 1) (x - 2) (x - 3) = 0
x - 1 = 0; x - 2 = 0; x - 3 = 0
x = 1; x = 2; x = 3
Y-intercept: To find the y-intercept, substitute x = 0.
Then y = 3 (0 - 1) (0 - 2) (0 - 3) = -18.
Answer: The x-intercepts are (1, 0), (2, 0), and (3, 0); and the y-intercept is (0, -18).
-
Example 2: Find the end behavior of the cubic function that is mentioned in Example 1.
Solution:
The given function is, f(x) = 3 (x - 1) (x - 2) (x - 3).
Here, the leading coefficient is 3 > 0.
So its end behavior is:
f(x) → ∞ as x → ∞ and
f(x) → -∞ as x → -∞Answer: f(x) → ∞ as x → ∞ and f(x) → -∞ as x → -∞.
-
Example 3: Find the critical points of the cubic function that is mentioned in Example 1.
Solution:
Given that f(x) = 3 (x - 1) (x - 2) (x - 3) = 3x3 - 18x2 + 33x - 18.
For critical points,
f'(x) = 0
9x2 - 36x + 33 = 0
Dividing both sides by 3,
3x2 - 12x + 11 = 0
Using the quadratic formula,
x = (12 ± √144 - 132) / (6) ≈ 1.423 and 2.577
Answer: The critical points are at x = 1.423 and x = 2.577.

FAQs on Cubic Function
What is the Standard Form of a Cube Function?
A cube function is a third-degree polynomial function. It is of the form f(x) = ax3 + bx2 + cx + d, where a ≠ 0.
What is Cubic Function Equation?
A cubic function equation is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, and d are constants (or real numbers) and a ≠ 0.
How do You Determine a Cubic Function?
A function having an expression with a cube of the x variable can be a cubic function. If a function is of the form f(x) = ax3 + bx2 + cx + d, then it is called a cubic function. Here, a, b, c, d can be any constants but take care that a ≠ 0. Any of the b, c, or d can be a zero.
How to Find the Intercepts of a Cubic Function?
For any cubic function y = f(x):
- The x-intercepts are obtained by substituting y = 0.
- The y-intercepts are obtained by substituting x = 0.
What is the Process of Graphing Cubic Function?
Here is the process of graphing a cubic function.
- Find the intercepts.
- Find the critical points.
- Find the end behaviour.
- Find some points on the curve using the given function.
- Plot all the above information and join them by a smooth curve.
How Many Real Zeros a Cube Function Have?
A cube function can have 1 or 3 real zeros. This is because
- The degree of cubic function is 3.
- Complex zeros occur in pairs.
How Many Complex Zeros a Cubic Function Have?
A cubic function can have 0 or 2 complex zeros. This is because
- The degree of cubic function is 3 and so it has a maximum of 3 roots.
- Complex zeros occur in pairs.
How to Sketch a Cube Function?
To sketch a cube function:
- Plot the x-intercepts.
- Plot the y-intercept.
- Plot the critical points.
- Join them by all by taking care of the end behavior.
visual curriculum
