A day full of math games & activities. Find one near you.

Interval Notation

Interval notation is a method to represent an interval on a number line. In other words, it is a way of writing subsets of the real number line. An interval comprises the numbers lying between two specific given numbers. For example, the set of numbers x satisfying 0 ≤ x ≤ 5 is an interval that contains 0, 5, and all numbers between 0 and 5.

Let us understand the interval notation and different types of intervals in detail using solved examples.

1.	What is Interval Notation?
2.	Different Types Of Intervals
3.	Notations For Different Types of Intervals
4.	Number Line Representation of Different Types of Intervals
5.	Converting Inequality To Interval Notation
6.	FAQs on Interval Notation

What is Interval Notation?

Interval Notation is a way of expressing a subset of real numbers by the numbers that bound them. We can use this notation to represent inequalities. We know an interval expressed as 1 < x < 5 denotes a set of numbers lying between 1 and 5.

Examples of Interval Notation

Suppose we want to express the set of real numbers {x |-2 < x < 5} using an interval. This can be expressed as interval notation (-2, 5).

The set of real numbers can be expressed as (-∞, ∞).

Different Types Of Intervals

Intervals can be classified based on the numbers the set comprises. Some sets include the endpoints specified in the notation, while some might partially or not include the endpoints. In general, there are three types of intervals given as,

Open Interval
Closed Interval
Half-Open Interval

Open Interval

This type of interval does not include the endpoints of the inequality. For example, the set {x | -3 < x < 1} does not include the endpoints, -3 and 1. This is expressed using open interval notation: (-3, 1).

Closed Interval

This type of interval includes the endpoints of the inequality. For example, the set {x | -3 ≤ x ≤ 1} include the endpoints, -3 and 1. This is expressed using closed interval notation: [-3,1].

Half-Open Interval

This type of interval includes only one of the endpoints of the inequality. For example, the set {x | -3 ≤ x < 1} include the endpoint -3. This is expressed using half-open interval notation: [-3,1)

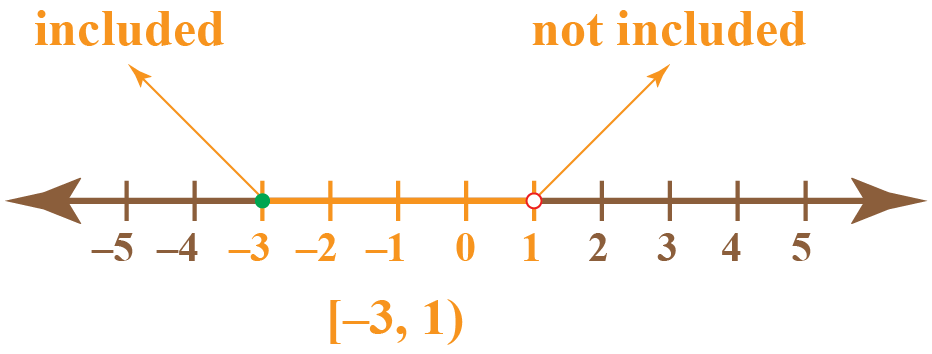
Notations For Different Types of Intervals

We can follow certain rules and symbols to represent the interval notation for different types of intervals. Let us understand different symbols that can be used to write a particular type of interval.

Symbol for Interval Notation

The notations we use for different intervals are:

[ ]: This is a square bracket that is used when both the endpoints are included in the set.
( ): This is a round bracket that is used when both the endpoints are excluded in the set.
( ]: This is a semi-open bracket that is used when the left endpoint is excluded and the right endpoint is included in the set.
[ ): This is also a semi-open bracket that is used when the left endpoint is included and the right endpoint is excluded in the set.

Number Line Representation of Different Types Of Intervals

Different types of interval notation can be represented on a number line. Look at the handy table that distinguishes between all the types of intervals using their representation on a number line.

Interval Notation	Inequality	Type of Interval
(a, b)	{x \| a < x < b}	Open Interval
[a, b]	{x \| a ≤ x ≤ b}	Closed interval
[a, ∞)	{x \| x ≥ a}	Half-Open Interval
(a, ∞)	{x \| x > a}	Half-Open Interval
(-∞, a)	{x \| x < a}	Half-Open Interval
(-∞, a]	{x \| x ≤ a}	Half-Open Interval

Converting Inequality to Interval Notation

Follow the steps mentioned below to convert an inequality to interval notation.

Graph the solution set of the interval on a number line.
Write the numbers in the interval notation with a smaller number appearing first on the number line on the left.
If the set is unbounded on the left, use the symbol "-∞" and if it is unbounded on right, use the symbol "∞".

Let's take a few examples of inequality and convert them to interval notation.

Inequality	Number Line	Interval Notation
x ≤ 3		(-∞, 3]
x < 5		(-∞, 5)
x ≥ 2		(2,∞]

Important Notes on Interval Notation:

Interval notation is used to express the set of inequalities.
There are 3 types of interval notation: open interval closed interval, and half-open interval.
The interval with no infinity symbol is called a bounded interval.
The interval containing the infinity symbol is called an unbounded interval.

Related Articles:

Examples on Interval Notation

Example 1: For a person to be elected as the president, he should be a minimum of 35 years old. Give an interval representing this information.

Solution:

Let's represent the age of the president by A.

It is given that the person's age A should be a minimum of 35

This means that A should be either greater than or equal to 35

Hence, this is represented by the inequality, A ≥ 35

So, the required interval is [35, ∞).
Example 2: For a school to participate in an Olympiad exam, the number of students from the school should be a minimum of 10. Represent this using an interval notation.

Solution:

Let x represent the number of students participating in a class, then x should be greater than or equal to 10

This means x ≥ 10

The interval notation is [10, ∞).

So, the number of students is represented by [10, ∞).
Example 3: Lola needs at least 1500 calories a day but the calorie intake should not exceed 1800 calories. Represent the possible amount of calories she could eat using interval notation.

Solution:

Let's represent the number of calories by x.

The inequality representing the possible amount of calories is given by 1500 ≤ x ≤ 1800

The interval notation for this inequality is [1500, 1800]

The required interval notation is [1500, 1800].

go to slide go to slide go to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Practice Questions on Interval Notation

go to slide go to slide

FAQs on Interval Notation

What do you Mean by Interval Notation?

Interval notation is a method to represent any subset of the real number line. We use different symbols based on the type of interval to write its notation. For example, the set of numbers x satisfying 1 ≤ x ≤ 6 is an interval that contains 1, 6, and all numbers between 1 and 6.

What is Interval Notation on a Graph?

When we represent the solution set of an interval on a number line, that is a graph for the interval notation.

How to Graph Interval Notation using Number Line?

We can graph the interval notation for a given set of numbers based on the type of number and specific symbols for the brackets used to enclose the set for the given particular type.

What is the ∪ Symbol for Interval Notation?

The union "∪" symbol is used to denote the union of two or more intervals in any Interval notation. Interval notation is defined as the method used to represent any subset of the real number line.

What are the Types of Intervals?

There are different types of intervals that can be represented by following a different set of rules for interval notation. These types of interval notation can be given as,

Open Interval
Closed Interval
Half-Open Interval

How to Convert Inequality to Interval Notation?

We can convert inequality to interval notation using the below-given steps,

Firstly, we need to graph the solution set of the interval on a number line.
Then write the numbers in the interval notation with a smaller number appearing first on the number line on the left.
Use the symbol "-∞" for the unbounded set on left and if it is unbounded on right, use the symbol "∞".

How do you Exclude Numbers in Interval Notation?

We use the round brackets to exclude numbers in interval notation. These numbers are generally the endpoints of the given set. To exclude a set of numbers in between, we can use two different sets and club them together using the union symbol '∪'.

Download FREE Study Materials

Algebra Worksheets

Math worksheets and
visual curriculum