a^2 + b^2 Formula
To calculate the sum of two squares in an expression, the a^2 + b^2 formula is used. The a2 + b2 formula can be easily derived using the (a + b)2 or (a - b)2 formula.
- a2 + b2 = (a + b)2 - 2ab
- a2 + b2 = (a - b)2 + 2ab
Let us learn these along with a few solved examples in the upcoming sections.
What is the a^2 + b^2 Formula?
The a^2 + b^2 formula is used to calculate the sum of two or more squares in an expression. Thus, a sum of squares formula or a^2 + b^2 formula can be expressed as:
a2 + b2 = (a +b)2 - 2ab (or) a2 + b2 = (a - b)2 + 2ab
where, a, b = arbitrary numbers.
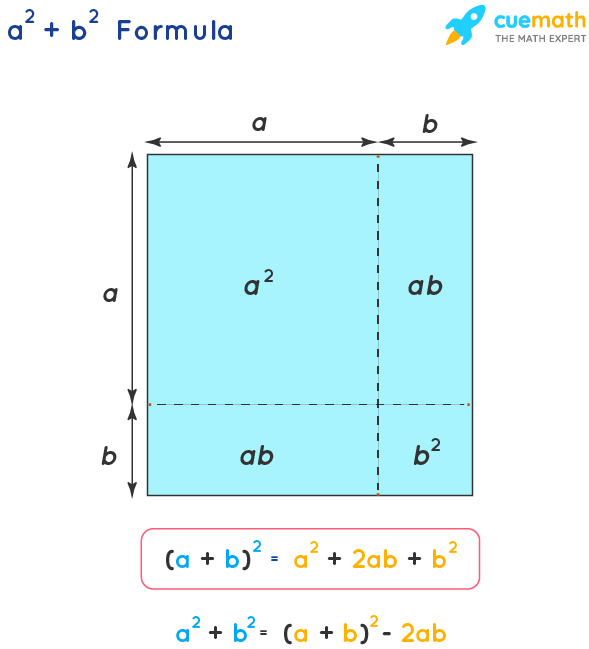
Let a and b be the two numbers, the squares of a and b are a2 and b2. The sum of the squares of a and b is a2 plus b2. We could obtain a formula using the known algebraic identity (a + b)2 = a2 + b2 + 2ab. On subtracting 2ab from both the sides we can conclude that a2 + b2 = (a + b)2 - 2ab.
Similarly, we can also prove that, a2 + b2 = (a - b)2 + 2ab.
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Example on a Square + b Square Formula
Example 1: Using the sum of squares formula, find the value of 52 + 62?
Solution:
To find : value of 52 + 62
Given: a = 5, b = 6
Using
a square plus b square formula Formula,
a2 + b2 = (a + b)2 - 2ab
52 + 62 = (5 + 6)2 - 2(5)(6)
= 121 − 2(30)
= 121 − 60
= 61
Answer: The value of 52 + 62 is 61.
Example 2: Verify that the value of x2 + y2 is (x + y)2 - 2xy using a2 + b2 formula.
Solution: To verify x2 + y2 = (x + y)2 - 2xy
Let us use the a square + b square formula,
a = x, b = y
Using the (a + b)2 formula let us expand the initial terms.
(a + b)2 = a2 + b2 + 2ab
Let us substitute the value of a and b as x and y
(x + y)2 = x2 + y2 + 2xy
On subtracting 2xy from both the sides,
x2 + y2 = (x + y)2 - 2xy
Answer: Hence verified
Example 3: Find the sum of the squares of 10 and 20 directly and use the a^2 + b^2 formula. Verify your answers.
Solution:
102 + 202 = 100 + 400 = 500
Using the formula of a square + b square:
a2 + b2 = (a + b)2 - 2ab, we get
102 + 202 = (10 + 20)2 - 2 × 10 × 20
= 900 - 400
= 500
Thus verified.
FAQs on a2 + b2 Formula
What is the Expansion of a2 + b2 Formula?
a2 + b2 formula is known as the sum of squares formula it is read as a square plus b square. Its expansion is expressed as a2 + b2 = (a + b)2 - 2ab.
☛Also Check: a^2-b^2 Formula
How To Simplify Numbers Using the a2 + b2 Formula?
Let us understand the use of the a2 + b2 a2 + b2 formula with the help of the following example.
Example: Find the value of 202 + 302 using the a2 + b2 formula.
To find: 202 + 302
Let us assume that a = 20 and b = 30.
We will substitute these in the formula of the sum of squares formula that is, a2 + b2
a2 + b2 = (a +b)2 - 2ab
202+302 = (20+30)2 - 2(20)(30)
= 2500 - 1200 = 1300
Answer: 202 + 302 = 1300.
What is the Formula of a Square + b Square in Algebra?
The a square plus b square formula is one of the important algebraic identities. It is represented by a2 + b2 and is read as a square plus b square. The (a2 + b2) formula is expressed as a2 + b2 = (a + b)2 - 2ab.
How To Use the a^2 + b^2 Formula?
We have two a2 + b2 formulas and we need to choose the relevant formula depending upon the available information.
- a2 + b2 = (a + b)2 - 2ab
- a2 + b2 = (a - b)2 + 2ab
What is the Difference Between a Square + b Square and a Square - b Square Formulas?
- a square plus b square formula is: a2 + b2 = (a + b)2 - 2ab (or) (a - b)2 + 2ab
- a square minus b square formula is: a2 - b2 = (a - b) (a + b)
visual curriculum
